Keeping Data Safe: Introduction to Encryption
Encryption is used to protect data (Oleksandr Pupko, iStockphoto)

Encryption is used to protect data (Oleksandr Pupko, iStockphoto)
Learn about the branch of mathematics involved with keeping data safe known as encryption.
Introduction
There are many different kinds of mathematics. Each helps people know and do different things. For example, arithmetic deals with numbers and basic operations such as adding, subtracting and multiplying. Algebra helps us figure out unknown quantities and geometry helps us understand shapes. But did you know that you can use math to hide things? You can, using something called encryption. Let’s see how it works.
Encryption
Imagine you wanted to send a secret message to a friend. How could you keep the message secret? You could try to give it to them without being seen. But what if you were caught and someone else saw the message? Not good! A better way would be to write the message in such a way that if someone other than your friend found it, they would not be able to or to read it. This is what encryption is all about.
Did you know?
Encryption is the term for creating secret messages. Decryption is the term for reading secret messages.
People want to send secret messages for many reasons. One of the most important ones is to keep other people from knowing what you are doing. For example, during a war, you would not want the enemy to know what you were up to. By encrypting your messages, you could keep them safe if they fell into enemy hands.
During World War II, encryption and decryption centres were set up across many countries. A very famous one was Bletchley Park in England. There, cryptologists worked hard to decrypt messages from the countries they were fighting.
A famous German cryptography machine created during World War II was called the Enigma machine. Enigma machines used a keyboard, a set of rotating disks and electric circuits to create the secret codes. The electrical pathway from each letter on the keyboard to the output letter was changed often. This made it a tough code to break. Eventually, information about the machines and the hard work of Allied cryptologists enabled the Allies to read the German coded messages. This ability to find out what the Germans were up to, without their knowledge, helped the Allies win World War III.
Try This!
You can make your own enigma machine using a Pringles can and this printout.
Substitution Codes
The Enigma machine worked by substituting one letter with another. This is called a substitution code. A substitution code is a code in which each letter in a word gets replaced by a different letter or symbol.
For example, if you wanted to send your bank password - “hotdog” - to a friend in a secure way, you could rewrite it using a substitution code such as “©¢¿£¢>”. Your friend would only be able to decode this message if they knew how you were substituting the letters.
Question 1:
Given the example above (“hotdog” is coded as “©¢¿£¢>”), what would your friend need to know in order to break the code (known as the encryption key)? The answer is at the end of the Backgrounder.
Another way to do a substitution code is to replace each letter of the message with a letter that is located a fixed distance from that letter in the alphabet.
For example the word DANGER becomes GDQJHU if we use the corresponding letter located three positions further along in the alphabet. This kind of encryption is called the Caesar Shift Cipher because Julius Caesar used it in Ancient Rome in relaying his messages.
Question 2:
Create a Caesar Shift Cipher for “The troops are approaching” and get a friend to solve it by giving him/her your encryption key. A potential answer is at the end of the Backgrounder.
In the “hotdog” example, if someone got a hold of the message, that person would have to figure out what substitution code you were using. For example, which letter does “¢” stand for? The person might have to try all the possible combinations before finding one that makes sense. However, there are some tricks that could make the job easier.
A code-breaker could use clues like the number of times a symbol appears in the secret message. Since the letter “e” is the most common letter in the English language, the most common symbol in a secret message probably stands for “e”. Figuring out a message this way is called Frequency Analysis. The trouble with frequency analysis is that it only works when the message is long.
So, how can you prevent someone from using frequency analysis to decode your secret messages? One possible solution to this problem is to use different substitution codes for different parts of the message. For example, in the first sentence of the message, “e” could be coded to “%”, and in the second sentence, “e” could be coded to “*.” If you change codes often enough, as the Germans did with the Enigma machine, it will be very difficult to find patterns.
Encryption Keys
The information that only you and the person reading your code know is called the encryption key of the code. This is because it allows you to ‘unlock’ its secrets. For example, in a substitution code, the key is the substitution pattern you agree on with your friend.
One simple type of encryption using keys is called Symmetric-Key encryption. In this method, a key is used to encrypt the message and the same key is used to decrypt the message.
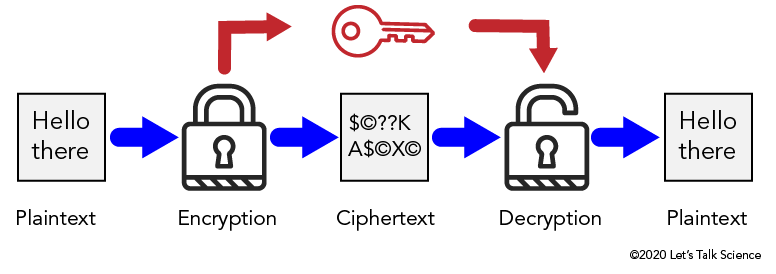
Image - Text Version
Shown is a colour diagram illustrating the process of Symmetric-Key encryption.
The diagram is laid out horizontally, with arrows indicating steps in a process from left to right.
The first image on the left is a pale grey box containing the text "Hello there." This is labelled below as "Plaintext."
A blue arrow points from here to an illustration of a locked padlock. This is labelled "Encryption."
Another blue arrow points from here to pale grey box containing a series of characters. These are a dollar sign, a copyright symbol, two question marks, a capital letter K, a capital letter A, a dollar sign, a copyright symbol, a capital letter X, and another copyright symbol. This is labelled "Ciphertext."
Another blue arrow points from here to an illustration of an open padlock. This is labelled "Decryption."
The last blue arrow leads from here to a third grey box. This is identical to the first image. It contains the words "Hello there," and is labelled "Plaintext."
Above these images, a set of red arrows indicates another process. A red arrow leads from the locked padlock to an illustration of a key. A second red arrow leads from here to the open padlock.
In Symmetric key encryption, the original message is in what is known as plaintext. The message is then encrypted with the symmetric key which converts it to ciphertext. The ciphertext is decrypted with the symmetric key. Now the message can be read as plaintext.
Symmetric key encryption is a relatively simple method, which means it is fairly easy to break codes done this way.
Did you know?
A cryptologist is a person who studies codes.
A more tricky method is Public Key Encryption. In this method, two different keys are used. One key is used to encrypt the message. A different key is used to decrypt the message. The key used to encrypt the message is called the public key. The key used to decrypt the message is called the private key. These keys are mathematically linked in such a way that it is virtually impossible to guess the private key given the public one. Public key encryption is a safer method for encryption than symmetric key encryptions because only the intended reader knows the private key.
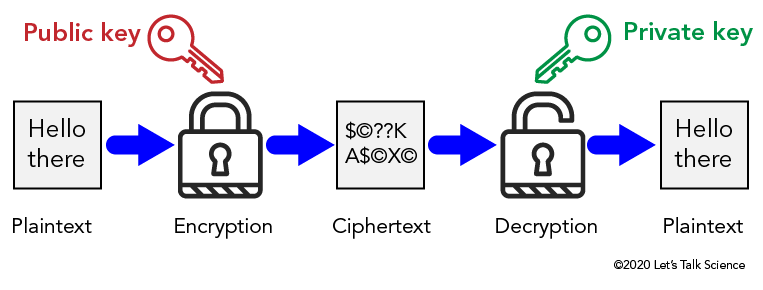
Image - Text Version
Shown is a colour diagram illustrating the process of Symmetric-Key encryption.
The diagram is laid out horizontally, with arrows indicating steps in a process from left to right.
The first image on the left is a pale grey box containing the text "Hello there." This is labelled below as "Plaintext."
A blue arrow points from here to an illustration of a locked padlock. This is labelled "Encryption." Above, a red illustration of a key is labelled "Public Key" in red letters.
Another blue arrow points from the locked padlock to a pale grey box containing a series of characters. These are a dollar sign, a copyright symbol, two question marks, a capital letter K, a capital letter A, a dollar sign, a copyright symbol, a capital letter X, and another copyright symbol. This is labelled "Ciphertext."
Another blue arrow points from here to an illustration of an open padlock. This is labelled "Decryption." Above, a green illustration of a key is labelled "Private key" in green.
The last blue arrow leads from the open padlock to a third grey box. This is identical to the first image. It contains the words "Hello there," and is labelled "Plaintext."
Compression Codes
Another type of code used by cryptologists is Compression code. Compression codes are a way of rewriting information using fewer characters. An advantage of this code is that it takes less space to store on a computer. Compression codes also help to transmit things more quickly over the Internet.
Imagine the secret message is:
Welcome to New Brunswick!
We could remove some of the characters in this message and still be able to read it. For example, if we remove all of the vowels in the message, we would get:
Wlcm t Nw Brnswck!
The message is shorter and the meaning is still fairly clear. This message only needs two-thirds of the original space to store on a computer. So, removing all of the vowels in an English message is a simple kind of compression code.
Other kinds of compression codes have been developed for other kinds of data. For example, JPEG is a method for compressing images.
Did you know?
JPEG stands for Joint Photographic Experts Group. This is the group who created this code.
Morse Code
Morse code is one of the most famous types of code. It was first demonstrated by Samuel Morse, its inventor, in 1844. He used it with his electric telegraph machine to transmit information over telegraph lines. Telegraph lines were wires used to transmit electrical signals over long distances.
In Morse Code, each letter of the alphabet is encoded as a different pattern of dots and dashes. Common letters are represented by short sequences. For example a single dot stands for “E”. Less common letters are represented by long sequences, for example “dash-dash-dot-dash” stands for “Q”. This pattern keeps transmissions as short as possible since shorter sequences will be used a lot and longer sequences only rarely. This makes Morse code a kind of compression code.
Did you know?
International Morse Code is a modern variation of Morse’s original code.

Image - Text Version
Shown is a colour illustration of English numbers and letters next to their equivalents in Morse Code.
The illustration is black text and symbols on a pale yellow background. The title, International Morse Code is at the top centre. Below the title is a list of five sentences:
1. The length of a dot is one unit.
2. A dash is three units.
3. The space between parts of the same letter is one unit.
4. The space between letters is three units.
5. The space between words is seven units.
The main part of the illustration is the alphabet, and the numbers from 0-9, with their equivalents in dots and dashes. These are arranged in two columns.
A = dot, dash
B = dash, dot, dot, dot
C = dash, dot, dash
D = dash, dot, dot
E = dot
F = dot, dot, dash, dot
G = dash, dash, dot
H = dot, dot, dot, dot
I = dot, dot
J = dot, dash, dash, dash
K = dash, dot, dash
L = dot, dash, dot, dot
M = dash, dash
N = dash, dot
O = dash, dash, dash
P = dot, dash, dash, dot
Q = dash, dash, dot, dash
R = dot, dash, dot
S = dot, dot, dot
T = dash
U = dot, dot, dash
V = dot, dot, dot, dash
W = dot, dash, dash
X = dash, dot, dot, dash
Y = dash, dot, dash, dash
Z = dash, dash, dot, dot
1 = dot, dash, dash, dash, dash
2 = dot, dot, dash, dash, dash
3 = dot, dot, dot, dash, dash
4 = dot, dot, dot, dot, dash
5 = dot, dot, dot, dot, dot
6 = dash, dot, dot, dot, dot
7 = dash, dash, dot, dot, dot
8 = dash, dash, dash, dot, dot
9 = dash, dash, dash, dash, dot
0 = dash, dash, dash, dash, dash
Question 3:
Decode this word in International Morse code. The answer is at the end of the Backgrounder.
•••• • •-•• •-•• ---
Run-length Coding

Image - Text Version
Shown is a colour photograph of a pale grey machine with 31 buttons, a phone receiver and two paper trays.
The machine has a rectangular front with a slightly curved surface. The first paper tray extends from behind the top edge. The second is in a long horizontal opening below the top edge. A phone receiver with a curled cord is set into the left side of the front. A long blue sticker printed with the words "Inkjet Fax" is along the right side. In the centre, there is a small, thin LCD screen. Underneath are the numbered buttons of a phone keypad, with additional silver buttons on both sides. On the bottom right are larger round buttons in pink, green and beige.
The images and text sent by a fax machine are first converted into black and white parts. The machine creates a fine grid and fills in any squares that are black. It then sends information indicating whether each square in the grid is black or white.
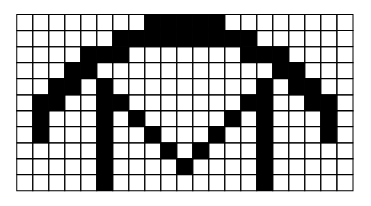
Image - Text Version
Shown is a black and white grid with with some squares filled in black to form an image.
The image is a grid of black lines on a white background. Some of the small squares in the grid are filled with black. These form a capital letter M with a curved line over the top.
Now let’s say the “0” represents a white pixel, and “1” represents a black pixel.
To send the first line of the picture, you could send the message:
000000001111100000000
This message is only 21 characters long!
Now let’s say each character takes one second to transmit. The description of the first line of the picture would take 21 seconds to transmit. This is not exactly fast. So, you might be wondering if there is a faster way to transmit the information.
Since the pictures sent by fax machines often contain long blocks of either white or black pixels, we could send a description of pixels as blocks. We only need to send a message saying how many pixels are contained in each block. This is called run-length coding.
In the picture above we could encode the first line as 8,5,8 which takes only 3 characters.
The system always assumes that you start with white pixels.
Question 4:
Encode the rest of the picture above in both regular coding (0s and 1s) and run length coding. The answer is at the end of the Backgrounder.
Now you know a few ways to hide messages using math!
Answers
Question 1:
Given the example above (“hotdog” is coded as “©¢¿£¢>”), what would your friend need to know in order to break the code (known as the encryption key)?
Answer:
Your friend would need to know that h = ©, o = ¢, t = ¿, d = £ and g = >.
Question 2:
Create a Caesar Shift Cipher for “The troops are approaching” and get a friend to solve it by giving him/her your encryption key.
Answer:
This will depend on the encryption key used. If you used a Caesar Shift Cipher that was a shift of three letters, the ciphertext would read, “Wkh wurrsv duh dssurdfkloj.”
Question 3:
Decode this word in International Morse code. •••• • •-•• •-•• ---
Answer:
•••• = h, • = e, •-•• = l, --- = o, therefore the word is “hello”
Question 4:
Encode the rest of the picture above in both regular coding (0s and 1s) and run length coding.
Regular coding Run-length coding
Line 2: 000000111111111000000 6, 9, 6
Line 3: 000011100000001110000 4, 3, 7, 3, 4
Line 4: 000110000000000011000 3, 2, 11, 2, 3
Line 5: 001101000000000101100 2, 2, 1, 1, 9, 1, 1, 2, 2
Line 6: 011001100000001100110 1, 2, 2, 2, 7, 2, 2, 2, 1
Line 7: 010001010000010100010 1, 1, 3, 1, 1, 1, 5, 1, 1, 1, 3, 1, 1
Line 8: 010001001000100100010 1, 1, 3, 1, 2, 1, 3, 1, 2, 1, 3, 1, 1
Line 9: 000001000101000100000 5, 1, 3, 1, 1, 1, 3, 1, 5
Line 10: 000001000010000100000 5, 1, 4, 1, 4, 1, 5
Line 11: 000001000000000100000 5, 1, 9, 1, 5
References
MathWorks. (n.d.). RunLength.
History.com. (2009, November 9). Morse code & the telegraph.
Jones, D. W. (n.d.). Data compression and encryption algorithms. University of Iowa.
Practical Cryptography. (n.d.). Simple substitution cipher.
The Editors of Encyclopaedia Britannica. (n.d.). Enigma.
Tyson, J. (n.d.). How encryption works. HowStuffWorks.