Combinatorics

Introduction

Mathematics, in a very basic sense, describes relationships between numbers and other measurable quantities. It is called the “language of science.” A strong understanding of mathematics is essential in order to develop a deep understanding of science.

There are many different branches in mathematics, each with many unique and fascinating aspects. In this backgrounder you will explore ways in which we use mathematics to understand how things can be arranged. This is known as combinatorics. We hope this gets you to think of mathematics in a whole new light!

Combinatorics

Combinatorics is a branch of mathematics that counts the number of ways we can arrange certain objects into sets and subsets.

Multiplication Principle

The multiplication principle is all about counting the different ways that things can be combined, without worrying about the order things are in. Here is a typical question:

A deli has 5 kinds of soup and 4 different sandwiches. How many different lunches can you have at the deli consisting of one soup and one sandwich?

The multiplication principle says: If one event (such as choosing a type of soup) can occur in x # of ways and a second event (such as choosing a type of sandwich) can occur in y # of ways, then the two events can occur together in x times y # of ways. In other words, we just multiply the possibilities!

So to answer the question above, you have five choices for soup (x = 5) and four choices for sandwiches (y=4), so there are x·y or 5x4=20 possible lunch combinations consisting of one soup and one sandwich. 

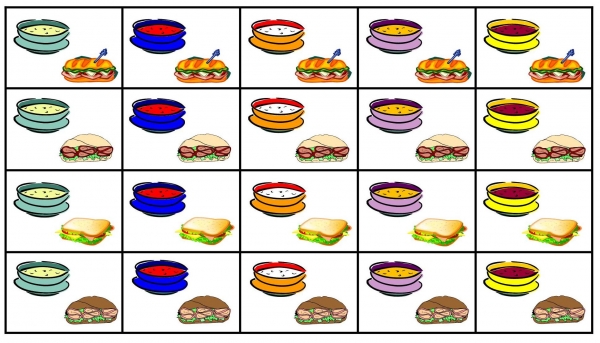
If there are more than two events, we can still use the multiplication principle. For example:

Here’s another example. Suppose you had a lock like the ones found on suitcases or used on some bicycle chains. It has a tumbler with three numbers. 

Each of the three spinning dials has the numbers 0 through 9. How many different three-digit numbers can be made using such a lock?

The first dial, or event, has 10 possible choices (0 through 9) (x=10), while the second dial also has 10 possible choices (y=10), as does the third dial (z=10). Using the multiplication principle, and assuming that any digit can appear on any dial, you have x·y·z = 10·10·10 = 1 000. There are 1 000 different possible combinations, which is another way of saying 1 000 different three digit numbers – which makes it tough for thieves to come up with the correct three-digit number using only trial and error!

Question 2

How many different licence plates can you make if the first three positions have letters of the alphabet and the second three positions have numbers? (Note: I, O and Q are not used). The answer is at the end of this backgrounder.

Here’s another example. Suppose Abdul, Bianca, Cho, and Dave make up a team of students in the Let’s Talk Science Challenge. There are four questions (1, 2, 3, 4), and each student must answer only one question. How many different ways can they take turns answering these questions?

As one possibility, they might go in order; so Abdul will answer question 1, Bianca question 2, and so on. As another possibility, Cho might go first, then Bianca, etc. Listing all the possibilities could quickly become boring!

Here’s a quicker way to figure it out: for question 1, there are four possible students who can answer it (Abdul, Bianca, Cho, and Dave). Once the team decides who will go first, that person cannot go again. This means there are three students left to answer question 2. Then, there will be two students left who can answer question 3, and the last remaining student is forced to answer the last question. Using the multiplication principle, there are 4·3·2·1=24 ways the students can answer the questions.

But wait, there is a pattern here. For instance, what if you were keen on planning what you were going to wear for school for the upcoming week. You had five favourite shirts. How many different ways could you lay out your shirts so that you wore one for Monday, a different one for Tuesday, a third for Wednesday, and so on through Friday? Using the multiplication principle, there are 5·4·3·2·1=120 ways to lay out your favourite shirts for the week. And you thought you had nothing to wear!

Now that you’ve got the idea, here is a little mathematical notation. Products that look like 9·8·7·6·5·4·3·2·1, with all of the numbers in descending order to 1, are called factorials. Instead of writing out 9·8·7·6·5·4·3·2·1, we can write 9!, which means the same thing (and takes up less space on the page). It’s also easier to say “nine factorial” than to say “9 times 8 times 7 times…,” So in our example with Abdul, Bianca, Cho, and Dave there are 4!=24 (“four factorial”) possibilities. In our last example with five shirts, there were 5! = 5·4·3·2·1 = 120 possibilities.

Answers