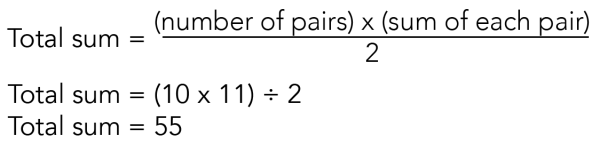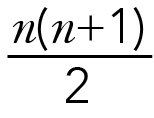Gauss Summation

Gauss Summation

The Gauss Summation is named for Johann Karl Friedrich Gauss. He was a German mathematician. Gauss is one of history’s most influential mathematical thinkers. A legend suggests that Gauss came up with a new method of summing sequences at a very young age. The legend says that his math teacher asked the class to add the numbers 1 to 100. In other words, the teacher wanted them to add 1 + 2 + 3 + 4 + 5… all the way up to 100!

The teacher assumed that this would take the students a very long time. Think about how long it would take you to add up all the numbers from 1 to 100 one by one. However, Gauss answered 5050 almost immediately. 

This story may not be entirely true. But, it reminds us that the youngest students are sometimes the ones to discover new mathematical patterns. Now, let’s think about the pattern that Gauss used to solve this problem quickly. 

The trick that Gauss used to solve this problem is that it doesn’t matter what order we add the numbers. No matter what order we follow, we will get the same result. 

For example:

2 + 3 has the same answer as 3 + 2.

We can reorder the numbers from 1 to 100 in a clever way. This can help us add them more quickly. Here is a simple example which will show you how this grouping strategy works. 

Say you wanted to add the numbers from 1 to 10.

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = ?

 

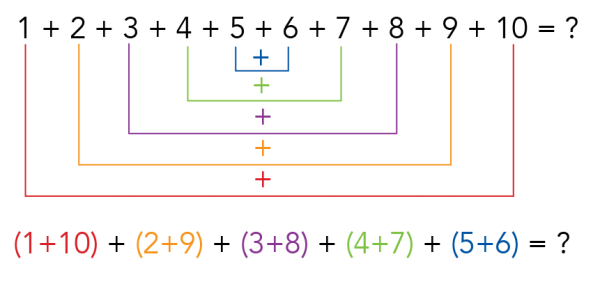
Now, you might have noticed something strange. Each of these pairs adds up to 11. So, we can think about our problem like this

(1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = ?

(11) + (11) + (11) + (11) + (11) = ?

Since we have 5 pairs, our answer is 

11 + 11 + 11 + 11 + 11 = 11 x 5 = 55

Well, this is getting somewhere! 

Let’s look at this in a different way. Instead of lining the numbers up in one row. Line up the numbers in two rows. In the first row the numbers go up. In the second row the numbers go down. For 1 to 10 it would look like this.

Image - Text Version

Numerals 1 to 10 are lined up in ascending order in the top row. Numerals 10 to 1 are lined up in descending order in the bottom row.

 

Now sum up each column.

Image - Text Version

Sum of each column is 11.

 

The total of all the numbers above is the number of pairs multiplied by the sum of each pair. But we only want the sum of one row, not both rows. So, we need to divide our answer by 2.

We can write this as: 

Image - Text Version

The sum is the number of pairs multiplied by the sum of each pair and that total is divided by 2. In our case, ten is multiplied by eleven and then divided by two. This give a final sum of 55.

 

We can use algebra to help us represent this pattern. Algebra uses letters and other symbols to represent numbers in equations. We can use the letter n to represent how many numbers are in our list. This is the largest number. For our example n would be 10. The number of pairs would be this number divided by 2. You will notice that the size of the pair is the number of pairs plus 1. So, we could write use n to write 

(number of pairs) x (sum of each pair) = n/2 x (n +1)

But remember, like before, we only want the sum of one row, not both. So we divide the formula above by 2 and get:

Image - Text Version

n outside a bracket followed by n plus one inside a bracket. This is divided by 2.

 

Can we do the same thing for a total that is an odd number, say 67? Try it yourself before looking at the answer below.

Real World Applications

This problem is an example of finding the sum of an arithmetic sequence. A sequence is a set of ordered numbers. In an arithmetic sequence, the distance between any two consecutive numbers is the same. We can use Gauss's method to find the sum of any arithmetic sequence.

 

Finding the sum of a sequence can help people solve a variety of real world problems. Businesses find the sum of sequences to estimate costs or revenue. Even calculating your taxi fare is the sum of an arithmetic sequence. You start with a base fare. Your total cost increases by the same amount every minute. 

Finding the sum of a sequence is also a common computer science question. Computer scientists use Gauss’s method to do this. The Missing Number question is a common technical interview question. Gauss’s method is needed to solve it. Many of these applications use complicated looking formulas. However, they are really just using Gauss’s method of finding the sum of a sequence. 

 

ANSWER

1 + 2 + 3 + 4……66 + 67 = ?

n = 67, n + 1 = 68

n(n + 1)/2

67 x 68/2

= 2 278