Introduction to Algebra

What is Algebra?

We are surrounded by unknown numbers. Imagine a closed bag of chips. Do you know how many chips are inside? Probably not without opening it and counting. A closed bag holds an unknown number of chips.

Image - Text Version

Shown is a cartoon illustration of a bag of potato chips. The bag is open and a number of chips are around and on top of the bag. The word "chips" is written on the bag.

 

There are lots of examples of numbers that we don’t know. Think about standing on a scale to weigh a suitcase. You know your own weight and the total weight, but you don’t yet know how much the suitcase weighs. Or imagine working as a babysitter. You might know how much you make each hour, but you probably don’t know how much you will make this year.

We call these unknown values variables. But what if we want to figure out the value of some of these variables? Luckily, there is a whole branch of math that can help us. It’s called algebra. In algebra, we work with unknown numbers to solve problems.

Did you know?

The word “algebra” comes from the Arabic word al-jabr. This term is translated as “reunion of broken parts.”

Like many good ideas, algebra was not developed by one person. Over many years, lots of different civilizations contributed to the development of algebra. This includes Babylonia, Egypt, Greece, China, and India.

Many people call Persian mathematician Muhammad Ibn Musa al-Khwarizmi the father of algebra. In ninth century Baghdad he combined and improved ideas from earlier generations. He wrote a famous book that continues to influence the techniques that we use today.

Image - Text Version

Shown is a colour photograph of a bronze statue outdoors near a mosque. The statue is of a reclining man wearing a turban and long, loose robes. He is supporting himself with his left hand and in his right hand is a piece of cloth. There are deep furrow lines on his forehead, which suggests he is thinking very seriously about something.

 

Writing Equations with Unknowns

In algebra, letters are used to represent unknown values. For example, we could say that there are x potato chips in the bag described at the beginning of this article. In this case “x” represents the number of potato chips. Letters stand for numbers that we don’t yet know.

Did you know?

X is often used in algebra because the Arabic term for “something” was translated with the Greek letter chi (χ). This was later replaced with the Latin letter x.

We use variables in equations. An equationequation is a way of expressing that two things are equal. We can think of the left and right sides of an equation like two sides of a scale. The equal sign shows that the two sides have the same value.

Example 1

Imagine a scale with 3 apples on one side and a paper bag with apples inside of it on the other. How many apples are in the paper bag? 

You may instinctively know that there are 3 apples in the bag. We can describe the number of apples in the bag using an equation like this:

x = 3

X is a placeholder for an unknown number of apples. We could also use any other letter such as:

b = 3 or y = 3

Image - Text Version

Shown is a colour illustration of a scale used as an analogue for an algebraic equation. The bronze scale has a paper bag hanging on the left side and three apples stacked in a pyramid on the right side. Between the two sides of the scale is a large blue equals sign.

 

Example 2

Now try writing an equation for the diagram on the right.

This diagram tells us that the apples in the bag plus one more apple are equivalent to four apples.

We can express this situation using the following equation.

x + 1 = 4

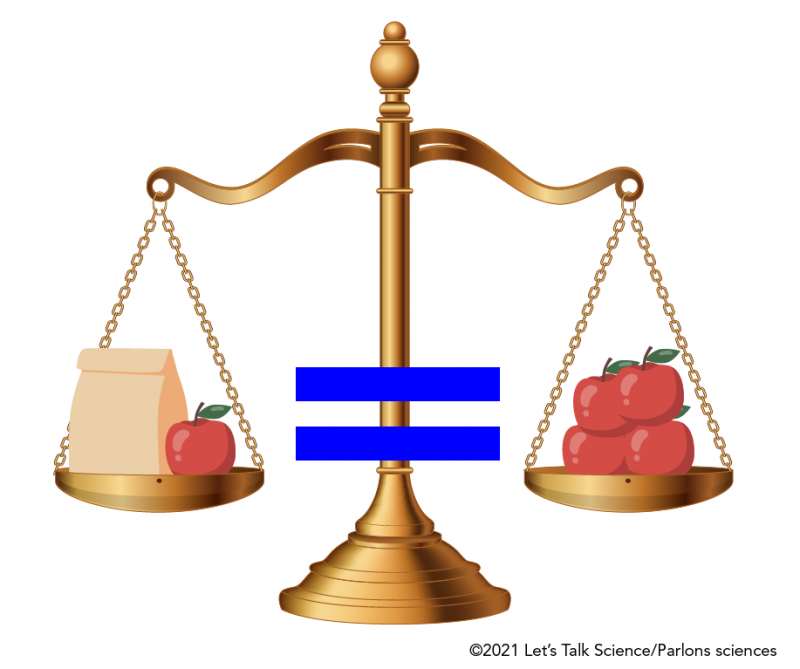
Image - Text Version

Shown is a colour illustration of a scale used as an analogue for an algebraic equation. The bronze scale has a paper bag and an apple hanging on the left side and four apples on the right side. Between the two sides of the scale is a large blue equals sign.

 

Example 3

Q1: Write an equation that represents the following diagram.

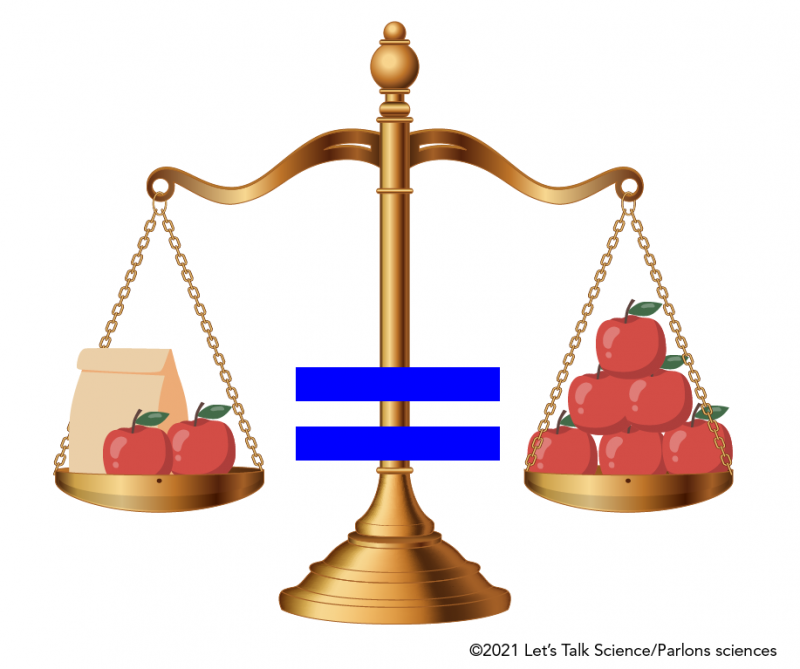
Image - Text Version

Shown is a colour illustration of a scale used as an analogue for an algebraic equation. The bronze scale has a paper bag and twp apples hanging on the left side and six apples on the right side. Between the two sides of the scale is a large blue equals sign.

 

Solving Equations With Unknowns

Now that we’ve written equations with unknowns, let’s solve them. Solving an algebraic equation means figuring out what number the variable represents. We do this by isolating the variable. This means that we want the variable to be the only value on one side of the equation. For example, in Example 1 the variable is isolated. X is all alone on one side of the scale. This makes it easy to see that x is equal to 3.

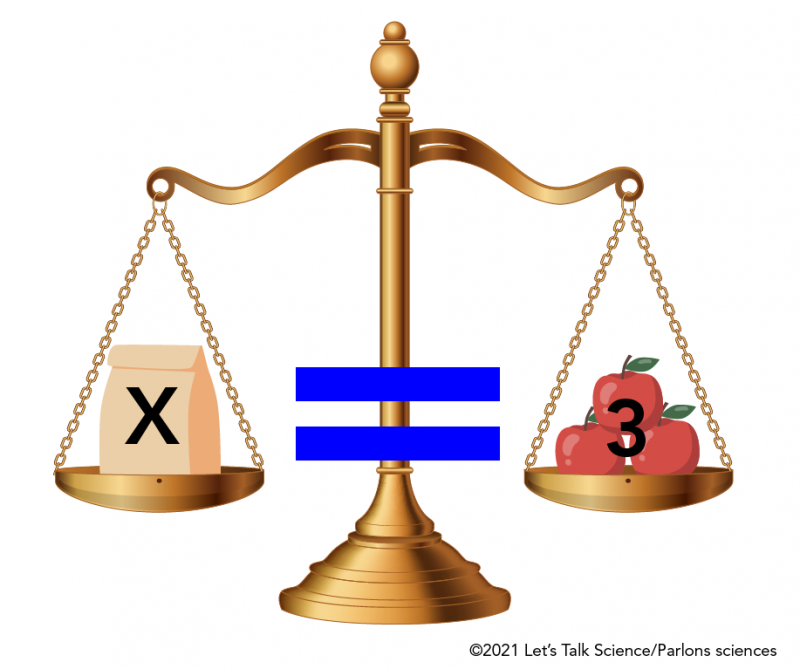
Image - Text Version

Shown is a colour illustration of a scale used as an analogue for an algebraic equation. The bronze scale has a paper bag hanging on the left side and three apples stacked in a pyramid on the right side. On the paper bag is an "x" and on the apples is a number 3. Between the two sides of the scale is a large blue equals sign.

 

Let’s isolate the variable in Example 2. Imagine moving the single apple on the left side of the scale to the right. We can represent this using subtraction. To keep the scale even, we need to follow one of the most important rules of solving algebraic equations. Always do the same thing to both sides of the equation.

So, if we subtract one from the left side, we must also subtract one from the right side.

X + 1 = 4

X + 1 - 1 = 4 - 1

X = 3

Image - Text Version

Shown is a colour illustration of a scale used as an analogue for an algebraic equation. The bronze scale has a paper bag hanging on the left side and three apples stacked in a pyramid on the right side. Above the left side of the scale is an apple and a minu sign. An apple and minus sign is also above the right side of the scale. Between the two sides of the scale is a large blue equals sign.

 

In both of these cases, we used subtraction to isolate the variable. This is because both original equations involved addition. Addition and subtraction are opposite operationsopposite operations. Multiplication and division are also opposite operations.

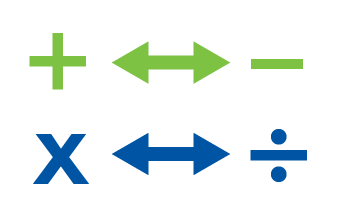
Image - Text Version

Shown is a colour illustration of opposite operations. The top row has a green plus sign and a minus sign with a double-ended arrow between them. The bottom row has a blue multiplication sign and a division sign with a double-ended arrow between them.

 

That brings us to our next rule of solving algebraic equations. Use the opposite operation to isolate a variable in an equation.

Let’s try using the opposite operation on another equation: 2c = 10. This equation involves multiplication. The opposite of multiplication is division. That means we need to divide both sides by whatever the variable is multiplied by. The division undoes the multiplication on the left side of the equation.

2c = 10 

2c ÷ 2 = 10 ÷ 2

c = 5

Try this same method to isolate the variables in the following equations.

Solving More Complex Equations

This process is even more useful when we need to solve complex equations. These equations involve more than one operation. We can use the same exact rules that we’ve learned. However, we may need to repeat the process multiple times.

For example, let’s solve this equation: 3x + 2 = 14. There are two operations in this equation, multiplication and addition. Because we are undoing operations, we use BEDMAS in reverse order. That means we undo first the addition and then the multiplication.

3x + 2  = 14

3x + 2 - 2 = 14 - 2

3x = 12

3x ÷ 3 = 12 ÷ 3

X = 4

Try a couple of these complex problems on your own. Remember the following steps.

1. Use BEDMAS in reverse order to decide which operation to tackle first.
2. Use the opposite operation to undo what is happening to the variable.
3. Do the same thing to both sides.
4. Repeat until the variable is isolated.

Algebra and Real World Situations

We can use algebra to solve all kinds of real world problems. This is where algebra becomes useful. The first and often most challenging step is to write a problem as an algebraic equation. Once you’ve written the equation, you can solve it using the same method that you used above. Let’s try the following problem.

Sofia opens a checking account and deposits $20. Every week, she adds an additional $5. How many weeks will it take her to save $300?

Image - Text Version

Shown is a colour photograph of a young asian girl holding a piggy bank. She is standing in front of a green blackboard with one large dollar sign and an equal sign on her left, and a plus sign with many small dollar signs on her right.

 

In this problem, our unknown value is the number of weeks. Let’s use the letter “w” to represent the number of weeks it will take Sofia to save $300. Now, let’s express this situation as an equation. Sofia starts with $20. Every week she adds $5. This means that she will end up with $20 and $5 times the number of weeks. We can write the equation like this:

20 + 5w = 300

Now let's figure out how many weeks.

20 + 5w = 300

20 + 5w -20 = 300 -20

5w = 280

W = 56

That means it will take Sofia 56 weeks to save $300 at this rate.

Try this same process to solve Question 7.

These same methods can be used to solve any number of complex problems. Scientists use algebra to represent situations in mathematical language. It is also the basis of other areas of math, such as geometrygeometry and calculuscalculus. Algebra is the basis for calculating the speed of a falling object, predicting the weather, and figuring out how much energy origami robots need to operate. Now that you know how to use this powerful way of thinking, who knows who you’ll discover!