Modular Arithmetic

We all learned to tell time when we were very young. It is something that we are familiar with. And for most people it is pretty easy. But, hidden behind this simple idea is a more complicated type of math called modular arithmetic. The idea goes like this.

What if you were going on a longer road trip? Perhaps to visit your grandparents in another province?

The point is that on a clock, we use a special way of counting. Once we get to 12 o’clock, the next hour is 1 o’clock, not 13 o’clock. And the next after that is 2 o’clock, not 14 o’clock. But this is just a choice of words. In reality, we could equally well say it was 14 o’clock or 2 o’clock. Either way we would mean 2 hours after 12 o’clock. In that sense, on a clock, 14 means the same thing as 2. 

Does that mean that 14 = 2? Maybe in a special way it does…

Congruent Modulo

We can think of it as ‘clock equals.’ Mathematicians have a special way of saying this. They say that two numbers are congruent modulo 12 if the difference between the two numbers is 12, 24, 36 or any other multiple of 12. For example, 2 and 14 are congruent modulo 12 because their difference, twelve, is divisible by 12. This means that on a clock, 2 and 14 mean the same thing. We express this mathematically as:

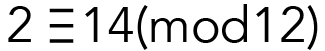
The mathematical symbol for congruence is ≡. Here, 2 and 14 are the numbers, and the number in brackets (12) is the modulus. Another example of two numbers being congruent modulo 12 is:

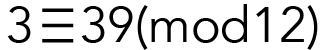
because the difference between 39 and 3 is 36, and 36 is divisible by 12. Not all numbers, however, are congruent modulo 12. For example:

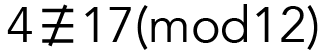
because the difference between 4 and 17 is 13, and 13 is not divisible by 12. 

Now imagine that we live in a world where the clocks have 7 hours instead
of 12. This may seem weird but it will give you a chance to try counting using modulo 7. In this way of counting, we say that two numbers are congruent modulo 7 if their difference is divisible by 7. For example:

because the difference between them (9 – 2 = 7) is divisible by 7. On the other hand,

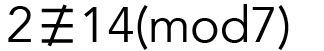
because the difference between them (14 – 2 = 12) is not divisible by 7.

Modulo Arithmetic

Let’s go back to our regular 12 hour clock. In the modulo 12 system, the answer to any calculation we do has to be less than 12. For example, the first problem in this section was 9+5. In regular arithmetic, we would say 9+5=14. In modulo 12 arithmetic, 14 is too big a number to be the answer (it doesn’t appear on a clock). We must, therefore, find its equivalent. 

Since we know that the number 14 is congruent with the number 2:

9 + 5 ≡ 2(mod12)

we give 2(mod12) as the correct answer for the question 9+5.

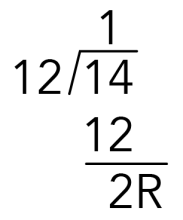
If the two numbers add up to exactly a multiple of the modulus, then you can write either a zero or the number before the modulus:

 3 + 4 ≡ 0(mod7)

OR 

 3 + 4 ≡ 7(mod7)

Mathematicians prefer to use zero, but 7 is also correct in the case above.

Try the following using modulo 7 arithmetic. Keep in mind that your answer should be between 0 and 6.

There is, in fact, nothing special about modulo 12 or modulo 7. We can choose any number to use as a modulus; for example, we could do math in modulo 5999 or 327 or 16 if we wanted to! 

Modular Arithmetic Applications

Modular arithmetic has many applications in cryptography and computer science. It’s often used to detect errors in identification numbers. Think about the kinds of identification numbers we use everyday. Credit cards, bank accounts, and product barcodes all involve long strings of numbers. These numbers need to be correctly exchanged by computer systems. Think about using your credit card to buy something online. Imagine if two of the digits were switched or typed improperly. Modular arithmetic is used to detect these kinds of errors. 

To help detect errors, many important numbers include a check digit. This is usually the last digit of a number. It is used as part of a modular arithmetic algorithm to check the number for errors. The mod 10 or Luhn algorithm is one that is commonly used. This algorithm involves doubling and then adding all of the digits up in a particular order. The number is correct if the total modulo 10 is equal to 0, meaning it is a multiple of 10. This algorithm is used to validate Canadian Social Insurance Numbers, credit card numbers, and many more. While we may not realize it, we use this kind of modular arithmetic application everyday. 

ANSWERS

Questions 1

Does 3 ≡ 9(mod7)?

3 ≢ 9(mod7)

No, because the difference between them (9 – 3 = 6) is not divisible by 7.

Questions 2

Does 1 ≡ 7(mod7)?

1 ≡ 7(mod7)

No, because the difference between them (7 – 1 = 6) is not divisible by 7.

Questions 3

Does 2 ≡ 16(mod7)?

2 ≡ 16(mod7)

Yes, because the difference between them (16 – 2 = 14) is divisible by 7.

Questions 4

Q103 + 18 = 0(mod7)

3 + 18 = 21 

21 ÷ 7 = 3R0. Since there is no remainder, we put a 0 in front of (mod7).

Questions 5

2 + 4 = 6(mod7)

2 + 4 = 6 

6 does not divide evenly by 7. In fact, it does not divide at all; therefore, it has a remainder of itself (6) which we put in front of (mod7).

Questions 6

19 + 10 = 1(mod7)

19 + 10 = 29

29 ÷ 7 = 4R1. We put the remainder of 1 in front of (mod7).