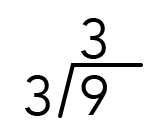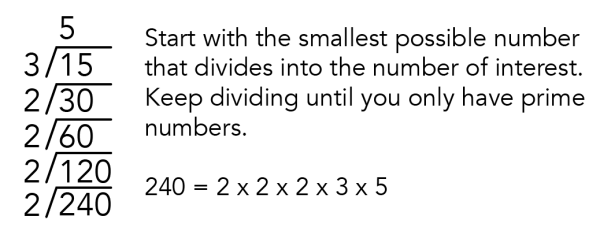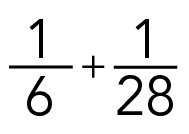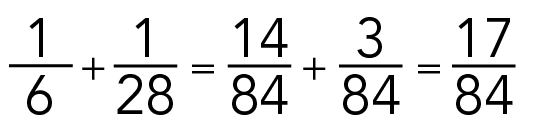Prime Factors

Prime Factorization

There are certain numbers that are the building blocks of all others. These special numbers are called prime numbers. A prime number, sometimes called a prime, is any number which can only be divided evenly by the number 1 and itself. That is, it cannot be divided by any number other than 1 and itself without leaving a remainder. 

The number 5, for example, is a prime number because the only numbers that divide evenly into it are 1 and 5. On the other hand, the number 6 is not a prime number because 6 ÷ 2 = 3. That is, both 2 and 3 are factors of 6. A factor is any number that can divide into another number evenly without leaving a remainder.

Did you know?

According to Goldbach’s Conjecture, every even whole number greater than 2 is the sum of two prime numbers. For example, 4 = 2 + 2 and 8 = 3 + 5. This conjecture is still unproven, but it has been tested up to 400,000,000,000,000.

Writing the prime factorization of a number means writing it as a product of primes. Let’s find the prime factorization of the number 12. Since 12 is not a prime number, it has at least one more factor; for example, 

3 is a factor of 12
Since 12 ÷ 3 = 4
So, we can write 12 = 4 x 3

 Is this a prime factorization? 

Well, 3 is a prime number, but 4 is not a prime number:
Since 4 = 2 x 2
So, we can write 12 = 2 x 2 x 3

All three numbers on the right side of this equation are now prime numbers. This means that we have succeeded in finding the prime factorization of 12!

You can find the prime factorization of any number using this method. Can you find the prime factorization of 8, and of 30? Try them yourself before looking at the answers. The answers are at the end of this backgrounder.

Drawing a division diagram can help you find the prime factorization of numbers. See the two examples below to learn how to draw a division diagram. Start at the bottom of the diagram by dividing the number of interest by the smallest possible prime number. The numbers making up the prime factorization will appear in a diagonal on the left side.

Example 1

Equation - Text Version

Long division showing how three divides into nine three times

Example 2

Equation - Text Version

Series of long divisions dividing prime numbers into 240. In this case, 240 can be divided by 2, 2, 2, 3 and 5.

There is only one prime factorization for any number. In other words, there is only one way to break up a number as a product of primes. 

Prime Factorization and Cyber Security

Did you know that you are using prime factorization every time you buy something online or sign into a bank account? Encryption technologies use prime factorization to protect sensitive information. These systems use the fact that it’s very challenging to factor large prime numbers back into primes. Mathematicians have been working on this problem for centuries. However, they still don’t have an efficient method of figuring out that 2,244,354 is (2 x 3 x 7 x 53,437). 

The RSA encryption algorithm makes use of this mathematical problem. In this method, two large prime numbers are multiplied to get an even large prime number. This new number is so large that no computer can figure out its prime factorization. The large prime number is public and can be seen by anyone. However, computers need the two original prime numbers to decrypt the message. 

This technology has been widely used for decades. However, new quantum computers are changing the field of cryptography. New quantum computers can factor prime numbers much more quickly than ordinary computers. Researchers are now having to find ways of making encryption quantum-proof. 

Least Common Multiple

Prime factorization can help us find Least Common Multiples (LCM). The LCM is the smallest positive number that is a multiple of two or more numbers. 

How do we find the least common multiple of two numbers? Well, we could list every multiple of each number until we find one in common. However, this would take a very long time. Prime factorization can help us find the LCM quickly and accurately. 

First, you need to write down the prime factorization of both numbers. For example, if you wanted to find the LCM of 6 and 28, you would write the prime factorizations:

6 = 2 x 3

28 = 2 x 2 x 7

Then, you look at how many times each prime number appears in the factorization of the first number. And how many times it is a factor of the second number. 

 

 

 

That is, the LCM of 6 and 28 equals 2 x 2 x 3 x 7 = 84. You can use this method to find the LCM of any pair of numbers. 

Least Common Multiple in Real Life

We often find the LCM to add or subtract fractions. We need a common denominator to add or subtract fractions. The common denominator is actually just the LCM of all the denominators. For example, say you wanted to add:

Image - Text Version

One sixth plus one twenty-eighth

 

In this case, the common denominator is the LCM of 6 and 28. We could use the method that we just learned to determine that the LCM is 84. We could then use this common denominator to add the fractions. 

Image - Text Version

One sixth plus one twenty-eighth equals fourteen eighty-fourths plus three eighty-fourths which equals seventeen eighty-fourths.

 

Finding the LCM can also help you solve many other real world problems. For example, the LCM can help you figure out when multiple repeating events will happen at the same time. Say two people running around a track at the same time. Person A takes 12 minutes to run a lap. Person B takes 18 minutes. We want to figure out how long it will take these two people to meet at the starting point. The answer to this question is the LCM of 12 and 18. We can use our method to figure out that these people will meet at the starting point after 36 minutes of running. 

Finding the least common multiple can also help us when we are buying multiple items that come in groups. For example, imagine you are preparing for a barbeque. You want to have the same number of cheese slices and buns. However, buns come in packs of 8, and cheese comes in packs of 6. Watch this video to see how finding the LCM can help you solve this problem. 

ANSWERS

Question 1:

2 is a factor of 8 

Since 8 ÷ 2 = 4 

So, we can write 8 = 4 x 2

But 4 is not a prime number since 4 = 2 x 2

So, we can write 8 = 2 x 2 x 2

 

Question 2:

2 is a factor of 30 

Since 30 ÷ 2 = 15 

So, we can write 30 = 2 x 15

But 15 is not a prime number since 15 = 3 x 5

So, we can write 30 = 2 x 3 x 5

 

Question 3:

The prime factorization of 18 = 2 x 3 x 3 and the prime factorization of 75 = 3 x 5 x 5

So, from 18 you can take two 3’s and a 2 

2 x 3 x 3

And from 75, since we already have one 3, you don’t need to take another one, but you do need to take the two 5

5 x 5

Put them together and you get 2 x 3 x 3 x 5 x 5 = 450