Triangles and Trigonometry

Everyone loves finding solutions to their problems, right? Think of the times when you solved a problem using fractions to make sure everyone has a fair share of cake or pizza. Now, imagine yourself in ancient times.

How could you calculate the boundaries of your land or cut pieces of stone perfectly to create a pyramid or temple? What tools would you use and what would you need to know about geometry? Geometry and algebra are two mathematical methods that help us solve problems.

The word geometry comes from the Greek words geos, meaning “earth,” and metron, meaning “measure.” Like this word, a lot of modern mathematical vocabulary comes from ancient Greece. However, historians are now finding evidence that principles of geometry were in use even earlier. We can see this in the case of a 3700 year old artifact from the Museum of Istanbul, which shows how land was split between landowners using geometry.

Image - Text Version

Shown is a colour photograph of an ancient clay tablet. The tablet is circular. It is on a black background. Near it are vertical and horizontal rulers showing the scale. The tablet has the identification number Si.427. The table has a break that runs approximately along the centre line. On the tablet are many sunken impressions. Some are lines that form a type of grid. Both within and surrounding the grid are triangular impressions that seem to be a form of early writing.

Geometry is the study of different spaces. But why is it important? How is geometry used outside of math class? In this backgrounder, we will look at these questions using only the simplest of thepolygons, the triangle.

Triangle Basics

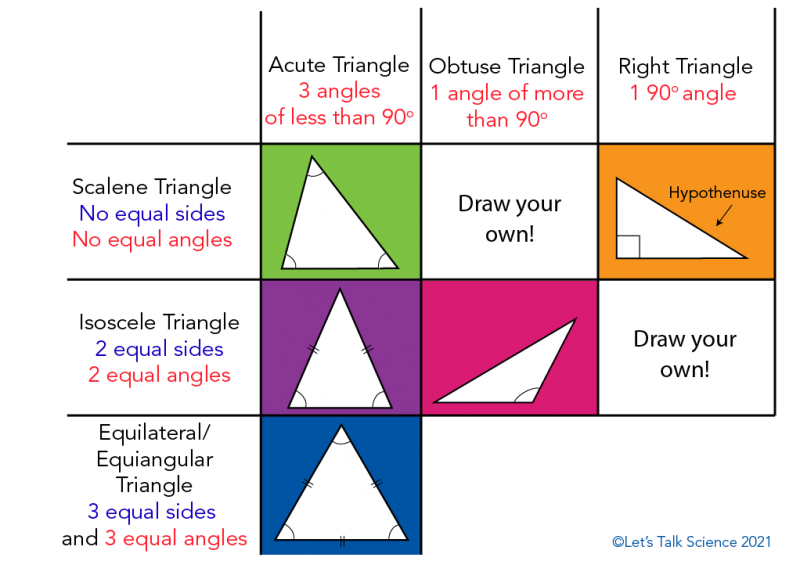
Let’s start with the basics. A triangle has three sides and three angles, thus its name, tri-angle, which means three angles. We can categorize triangles according to the lengths of their sides and the sizes of their internal angles.

Image - Text Version

Triangles can be grouped according to their sides and angles. Scalene triangles have no equal sides and no equal angles. Isosceles triangles have two equal sides and two equal angles. Equilateral triangles have three equal sides and three equal angles. Acute triangles have three angles of less than 90 degrees. Obtuse triangles have one angle of more than 90 degrees. Right angle triangles have one right angle. Some triangles can fit into more than one category.

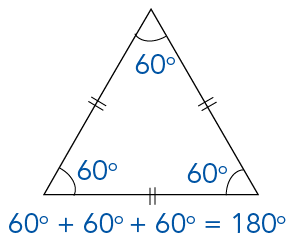
But comparing angles and sides of triangles is not that exciting. It gets more interesting when we start to see patterns that apply in certain situations. For instance, if we add up the three interior angles of a triangle, we always get a total of 180 degrees. This is actually the simplest form of the polygon interior angles rule. You can try this out at home. Take any triangle, measure its three angles and add them up to see for yourself!

Image - Text Version

Shown is a line drawing of an equilateral triangle. The triangle has three equal sides. These are identified using a small set of parallel lines that cross each side at the centre perpendicularly. The triangle also has interior angles of 60 degrees. These are identified using both text and an arched line in the interior of each corner. Along the bottom of the drawing is the equation 60 degrees + 60 degrees + 60 degrees = 180 degrees.

Pythagorean theorem

The pythagoreantheorem is one of the most well-known mathematical formulas. This pattern was first observed more than 2 000 years ago. A real person, named Pythagoras, wrote the rule that is still taught today to every student around the world!

The pythagorean theorem applies to all right angle triangles. Before learning the formula, watch the video on the left to better understand the logic behind it. If you’re still not convinced, watch the demonstration on the right! But first you need to know that the hypotenuse is the longest side of a right angle triangle and it is always the side opposite to the right angle.

So how is the formula, a² + b² = c², useful? There are many real-world applications, let’s look at a few of them.

How could you check that a piece of land is perfectly rectangular? Meaning, how can we make sure its four angles are 90 degrees? On paper, you might use a protractor but with large surfaces, that would not work.

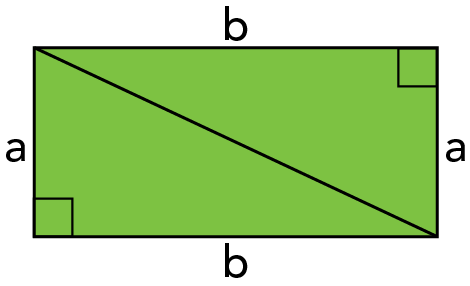
Let’s say that you cut the rectangle in 2 diagonally. What shapes would you get?

Image - Text Version

Shown is a colour illustration of a rectangle. The rectangle is green. Its width is about twice as much as its height. There is a diagonal line extending from the upper left corner to the lower right corner. The short sides are identified as “a” and the long sides as “b". Within the lower left and upper right corners are small squares that share a corner and sides with the rectangle. These squares are symbols that indicate the angle at the corner is 90 degrees.

That’s right, you get two right angle triangles with sides a and b of the same length. By knowing the lengths of a and b, you can use the pythagorean theorem to get the length of the hypotenuse, which is also thediagonalof the rectangle. Thus, no matter what shape of rectangle you start with, if you cut it diagonally, you will always get two right angle triangles. So how can you make sure the rectangle has all right angles? You simply need to measure the distance between both oppositevertices and they should be equal!

Land surveyors do this using a total station. This piece of equipment uses infrared signals and GPS systems to accurately measure angles and long distances. Surveyors place a target called a prism at the location that they want to measure. The prism contains a reflector. An infrared beam is pointed at the prism which reflects it back to the total station. Computers can then precisely measure angles and distances. 

Image - Text Version

Shown are two colour photographs.

The photo on the left is of a surveyor using a tool called a total station. The total station is a green, camera-like object . The three-legged tripod holds the device steady. The surveyor is a young adult woman with long blond hair and fair skin. She is wearing jeans, a purple sweatshirt and a black coat that is open at the front. Beside her on the ground is a red plastic case that is hinged in the middle. The woman is looking in the same direction as the total station is pointing. The surveyor is standing in a grassy field with small shrubs in autumn. Nearby is a row of small trees with no leaves. Beyond that, on the left, are lawns and the back side of several houses.

The photo on the right is a target sign that is used with a total station. The sign is a bright yellow rectangle. On it is printed a large black square within which are diagonal lines extending from the corners. At the centre, where the diagonal lines meet, is a circular red object. This is a prism that reflects the signal sent from the total station. In the background is a hill of pale grey rocks. Similar rocks and gravel are also in the foreground where the sign is located.

Trigonometry

Triangles are so fascinating that a branch of mathematics exists just to understand them! Trigonometry studies the relationships between the side lengths and angles in a triangle. “Trigonometry” might seem like a complex word, but let’s take a second to analyse it. Trigonometry comes from the ancient Greek words trigonon meaning “triangle” and metron meaning “measure.”

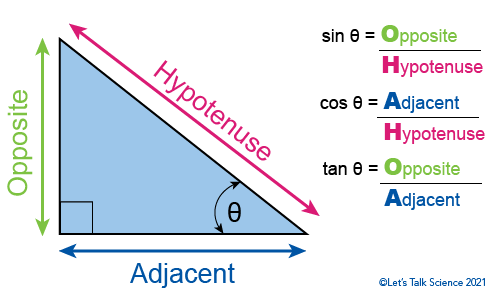
There are three main relationships, or functions, in trigonometry. They let you use two sides of a triangle to figure out the third. The functions are called Sine, Cosine and Tangent. These are usually abbreviated as sin, cos and tan.

Image - Text Version

Each side of a right angle triangle has a special name. The side opposite from the right angle is the hypotenuse. You can choose one of the other interior angles and call it 𝚹. The side that is beside 𝚹 is called the adjacent side. The side that is opposite 𝚹 is called the opposite side.

Triangulation

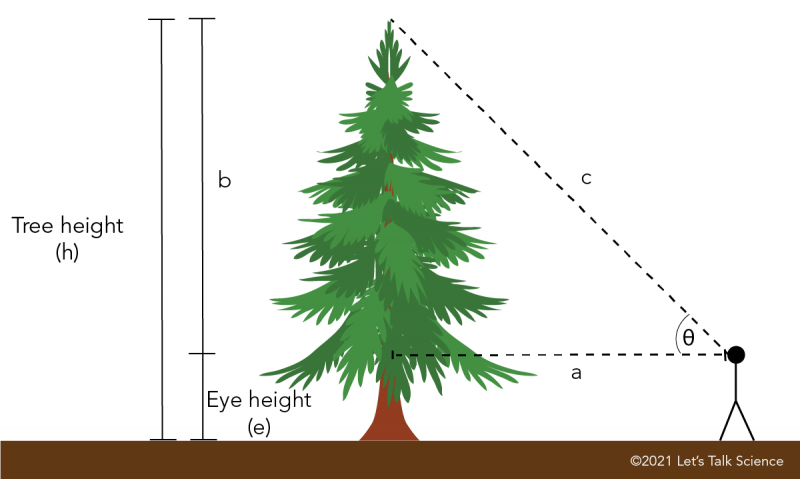
Triangulation in mapping and land surveying involves finding an unknown distance without measuring it directly. It does this using imaginary triangles! Triangulation is very useful when trying to measure tall objects. Climbing a tall tree to know its height is quite dangerous. However if you move away from the tree, you can take a few measurements to find its height.

Image - Text Version

When measuring a tree, there are several important angles and distances. The distance between yourself and the tree we could call a.This is the adjacent side of the triangle. The distance between your eye height and the top of the tree we could call b. This is the opposite side of the triangle. The sight line between your eye and the top of the tree we could call c. This is the hypotenuse of the triangle. The distance between the ground and your eye we could call e. The height of the tree h we could calculate by adding b plus e. 

 How to measure the height of a tree.

1. Measure the distance between yourself and the tree. This is labelled as a. a is the adjacent side of the triangle.
2. Find the angle between your eye height and the top of the tree. This is θ. You can find this angle using a digital inclinometer or a smart device app.
3. To calculate b, which is the opposite side, we need to use the formula
   tan θ = b/a
   and then use the cross multiplication method to find b.
   b = tan θ
   Even if you don’t know trigonometry, this can be done on a scientific calculator. To know the value of “tan θ”, input your angle and press the tan button.
4. Once you’ve calculated b, don’t forget to add the distance between the ground and your eye e to find the height of the tree h.

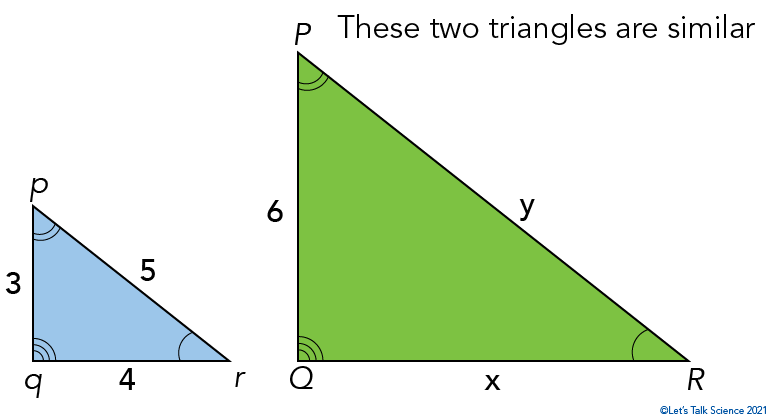
Another fun observation is when two right triangles are similar. In math, two shapes are similar if we simply need to flip, rotate or resize them to have the exact same triangle.

Look at the two similar triangles below. They are similar, so we can say:

Δpqr ∼ ΔPQR 

The ~ symbol means that the things are mathematically similar.

Image - Text Version

Two right angle triangles are shown. The blue triangle on the left is half the size of the green triangle on the right. The blue triangle has vertices p, q and r and side lengths of pq=3, qr=4 and pr=5. The green triangle has vertices P, Q and R and side lengths of PQ=6, QR=x and PR=y. ∠pqr ~ ∠PQR, ∠qpr ~ ∠QPR and ∠prq ~ ∠PRQ.

You can see that all angles are the same, but the lengths of the side are not. The interesting rule that can be used for similar triangles is that all their sides are proportional. That means that if we compare the sides as fractions, they will be equal.

pq = PQ qr    QR

qr = QR rp    RP

rp = RP pq   PQ

If we put in values, for the same side of each triangle, say for sides pq and PQ, we would get:

pq = 3 = 1
PQ   6    2

This common ratio is called the scale factor. In this case, the scale factor is 2.

Similarity and scale factor can be extended to other figures besides triangles.

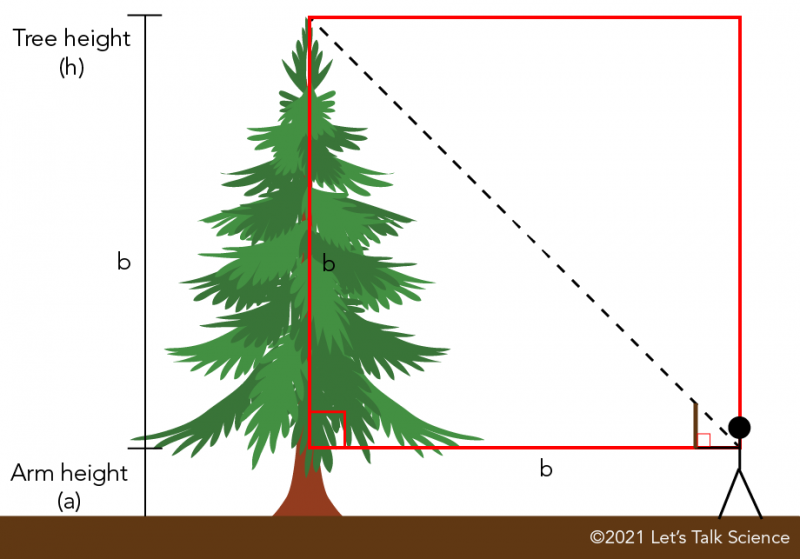
For example it can allow you to use an even simpler method to measure a tall tree. First you need to find a stick about the same length as your arm. Then you need to hold your arm out straight in front of you and hold the stick up at a right angle to your arm. While looking at the stick and the tree at the same time, walk backwards away from the tree until the top of the stick is at the same level as the top of the tree. The distance you have walked away from the tree, plus the height to your arm, is the height of the tree!

Why? Look at the diagram below. Can you see the two similar triangles? Now, can you see that the triangle formed with the stick is an isosceles triangle because the arm and the stick are the same length? Remember that an isosceles triangle has two equal sides and two equal angles. By creating similar triangles, you can measure some very large things!

You can also see how it is done by watching this video.

Image - Text Version

When you hold a stick the length of your arm upwards at a right angle, and imagine a line connecting the top of the stick to your shoulder, you would have an isosceles triangle. By standing at a distance away from a tree so that the top of the stick appears to be the same height as the top of the tree, you are creating an isosceles triangle with your body and the tree. This distance we can call b. This triangle is similar to the triangle that you made with your arm and the stick. To calculate the height of the tree h, you would add distance b to the distance from the ground to your arm a.

Triangulation in Maritime Navigation

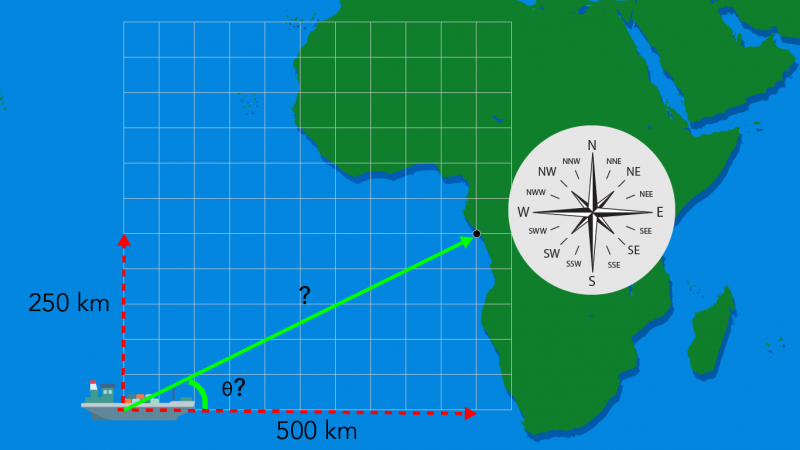
But finding the height is not the only time triangulation is useful. Let’s now consider maritime navigation. Imagine a ship that needs to travel to a point that’s 500 km to the east and 250 km to the north. In what direction should it go to travel the shortest distance possible? And how far would the ship travel?

Image - Text Version

A boat is out at sea. It is 500 km west and 250 km south of a point it is going to on the western coast of Africa. What is the shortest distance it would need to travel to this point and at what course should it travel?

 

Of course maritime navigation is a little more complex than this! A good navigator will need to take into account currents and winds, but the main direction will stay the same. The captain of the ship will need to adjust the route for those variables.

If you want to learn more about the connection between geometry and geography, make sure to read the backgrounder on Coordinates.

Triangles and Geographic Information Systems

Geometry plays an important role in Global Positioning Systems - better known as GPS. A satellite with a GPS system uses a form of geometry not unlike that used to calculate a right triangle. It uses the position of the satellite in the sky, the location of the GPS position on Earth identified by longitude and latitude, and the distance from that location to the place on Earth that equates to the satellite’s position in the sky. To learn more about how a GPS system works, check out the GPS backgrounder.

Triangulation in Computer Graphics

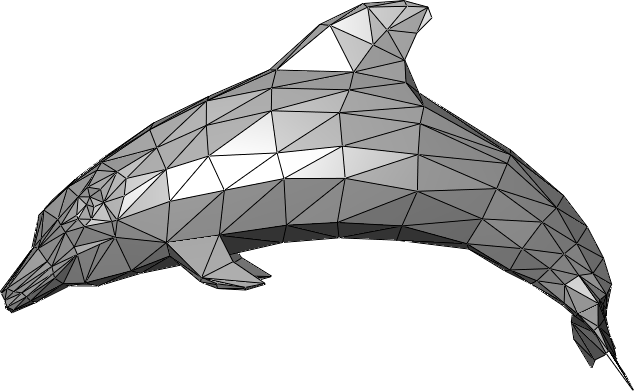
Another way to define triangulation is the decomposition of any surface into triangles. The dolphin image below is an example. This type of image is called a triangle mesh.

Image - Text Version

Shown is a grayscale illustration of a dolphin using a triangle mesh. The dolphin has a long banana-shaped body. It has a large fin on top with two smaller fins near the head on the lower part of the body. It has a wide, flat tail and a cone-shaped nose. The whole drawing is made using only triangles The triangles are filled with different shades of grey to give the sense of depth. Darker shades are below and lighter shades are on the top and side.below and lighter shades are on the top and side.

Triangle meshes are used a lot in 3D computer graphics such as in video games. Why? Because it takes less memory to turn surfaces into triangle equations. It’s also easier to change the shape of triangles than other shapes. That way, programmers can use software with pre-programmed algorithms to make characters move, without having to write the code from scratch!

ANSWERS

1. Answer for the similar triangles question:
   Since the scale factor is 2, x would be 4 x 2 = 8, and y would be 5 x 2 = 10
2. Answer for the maritime navigation question:
   1. Solving for the angle 𝚹.
      Let’s look at what information we have. We can see that the side of the triangle adjacent to 𝚹 is 500 km and the side opposite to 𝚹 is 250. If we look at the three trigonometry formulas, one has both opposite and adjacent in it. tan 𝚹 = opposite/adjacent
      Substituting in the values, we get tan 𝚹 = 250/500 = 0.5. So how do we get an angle from that?
      To solve for 𝚹 we need to take the inverse tangent of both sides.
      tan^-1 (tan 𝚹) = tan-¹(0.5)
      The tan^-1 cancels out the tan leaving us with:
      𝚹 = tan^-1(0.5)
      Using the tan^-1 on a calculator we get:
      𝚹 = 26.56 degrees.
   2. Solving for the distance (hypotenuse).
      For this, we can use the Pythagorean Theorem a² + b² = c²
      We know that a = 250 and b = 500
      Substituting into the equation we get:
      c² = 250² + 500².
      c² = 62 500 + 250 000
      c² = 312 500
      To solve for c, we take the square root of each side
      √c = √312 500
      c = 559
      That means the shortest distance the ship would need to travel would be 559 km.