The Math Behind GPS
Earth with pinned locations (Pure Imagination, iStockphoto)

Earth with pinned locations (Pure Imagination, iStockphoto)
How does this align with my curriculum?
Learn about the history and math behind the Global Positioning System.
Image - Text Version
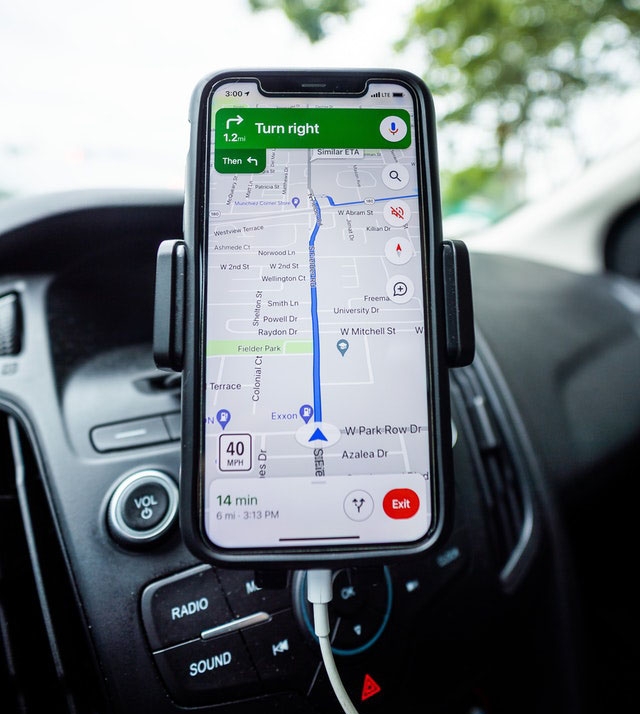
Shown is a colour photograph of a cell phone attached to the dashboard of a car. Visible on the phone is a map showing directions to a location.
Not only do we rely on GPS in our phones, it is also important for ships, planes, ambulances and so much more. However, many of us don’t know much about the math, science, and history of this technology. How can a system that fits inside a smartphone instantly pinpoint your location?
History of GPS
In the 1950's, researchers developed the first satellite navigation system for military purposes. After several decades of improvements, civilians began to use GPS in the 1980s. The system became fully functional in 1994. The United States government owns and maintains the Global Positioning System that we use in North America.
Image - Text Version
Image - Text Version
Shown is a black and white photograph of Sam Smith and Gladys West. Sam Smith is a middle-aged white man in a business suit. Gladys is a middle-aged black woman also in business attire. They are standing in an office in front of a desk covered in papers. Gladys is pointing at something on one of the pieces of paper with a pen in her hand. Sam is looking at what she is pointing at. Beside Gladys is a very large global on a pedestal.
Misconception Alert
Earth is not a perfect sphere. It has lumps and bumps which Gladys Mae West helped to model.
Roger Easton, Ivan Getting, and Bradford Parkinson also played key roles in the development of the GPS. These physicists and engineers developed ways to locate satellites and locations on Earth.
How does GPS work?
Before the development of GPS, people used a variety of different navigation techniques. Sailors often used the position of the stars to know what direction they were going.
Q1: What might be some problems with using stars to navigate?
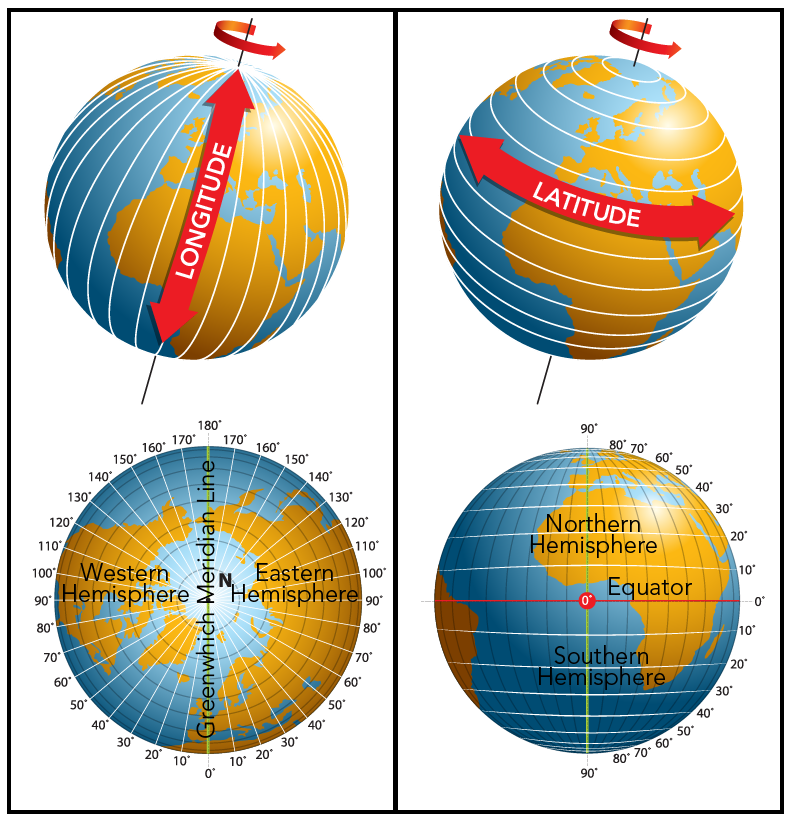
Navigation techniques help people find their latitude and longitude. Lines of longitude run from North to South. The line of 0º longitude runs through Greenwich, England. Lines of latitude run from East to West. The line of 0º latitude is the Equator. Knowing both your longitude and latitude gives your position on the globe.
Image - Text Version
Shown are four illustrations of the Earth showing the location and direction of the lines of longitude and latitude.
The Earth on the top left has white vertical lines circling the planet. These are identified as lines of longitude.
The Earth on the lower left shows a top-down view of the Earth. Lines of longitude are drawn using white lines that radiate outward from the north pole. They are marked and labelled in ten degree increments. The left side of the Earth is labelled as the Western Hemisphere and the right side of the Earth is labelled as the Eastern Hemisphere. Running vertically up the middle of the Earth is a line identified as the Greenwich Meridian Line.
The Earth on the top right has white parallel horizontal lines circling the planet. These are identified as lines of latitude.
The Earth on the lower right shows a side view of the Earth. Lines of latitude are drawn using parallel white lines. They are marked and labelled in ten degree increments. The upper part of the Earth is labelled as the Northern Hemisphere and the lower side of the Earth is labelled as the Southern Hemisphere. Running horizontally along the middle of the Earth is a line identified as the Equator.
Image - Text Version
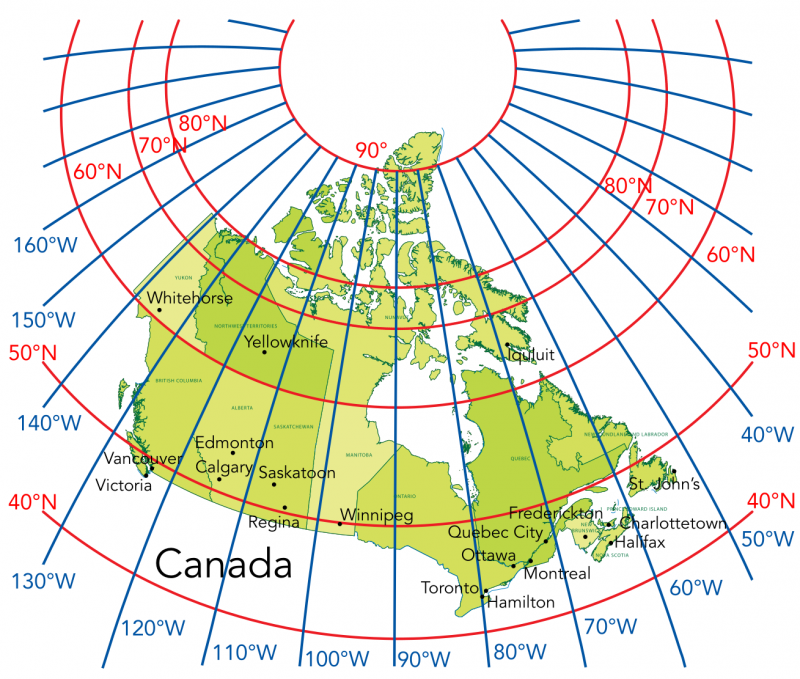
Shown is a map of Canada overlaid with lines of latitude and longitude. Lines of latitude are coloured red and lines of longitude are coloured blue. Major Canadian cities are also identified on the map.
Q2: At what latitude is Winnipeg located? At what longitude is Hamilton located?
Image - Text Version
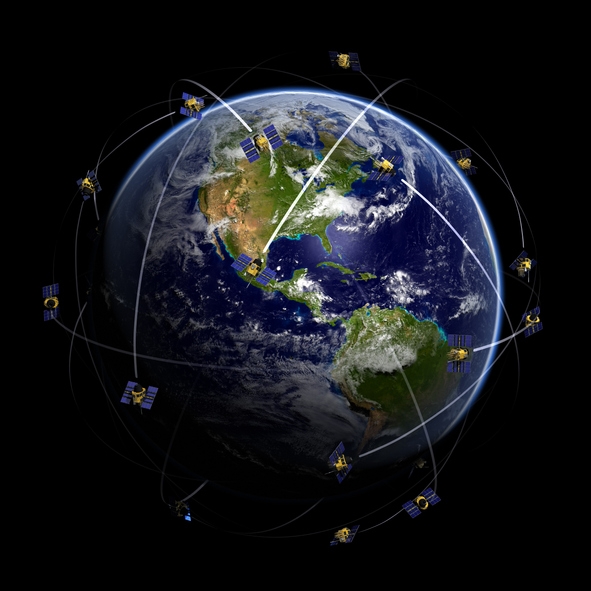
Shown is a colour illustration of the Earth in Space. Orbiting the Earth are around 20 tiny satellites. The direction of their motion is suggested using white streaks of colour behind each satellite.
Image - Text Version
Shown is an illustration of a satellite and cell phone.
The satellite is in the upper left part of the image. Radiating downward are parallel semi-circular lines that indicate that the satellite is sending down a signal to Earth. The cell phone is in the lower, central part of the image. Radiating upward are parallel semi-circular lines that indicate that the phone is sending up a signal to the satellite. Connected to the phone via a line is a small image of a map pin and a car to indicate that the phone uses the information for map apps and vehicle navigation systems.
A receiver uses the following formula:
Distance = signal speed x signal time
The signal speed is the speed of light (about 300,000,000 m/s). The signal time is how long it takes for the signal to travel from the satellite to the receiver. Multiplying these two numbers tells us the distance between the satellite and the receiver.
For example, imagine that it takes a signal 0.005 seconds to travel from a satellite from your phone.
Distance = 300,000,000 m/s x 0.005 s = 1,500,000 metres
That means that the satellite is 1.5 million metres or 1500 kilometres from the receiver.
Q3: How far from a receiver is a satellite if it takes 0.02 seconds for a signal traveling at the speed of light to reach the receiver? Give your answer in metres and kilometres.
Did you know?
GPS relies on Albert Einstein’s theory of relativity. The time information sent by satellites is adjusted to account for relativity. This makes the system more precise.
However, knowing how far away you are from one satellite doesn’t give you your position. For that, GPS uses trilateration.
Trilateration
Trilateration is a way of locating a point based on how far away it is from three other points. Multiple satellites must connect with the receiver to use this process. The distance between the receiver and several satellites is calculated. Trilateration is a method of using this distance information to find a location.
Misconception Alert
GPS uses trilateration not triangulation. Trilateration involves measuring distances. It is sometimes confused with triangulation which measures angles.
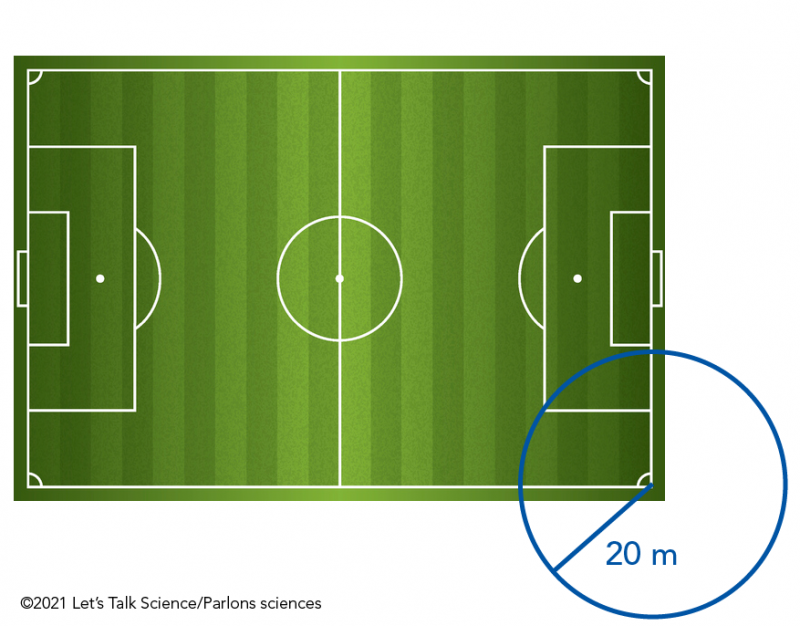
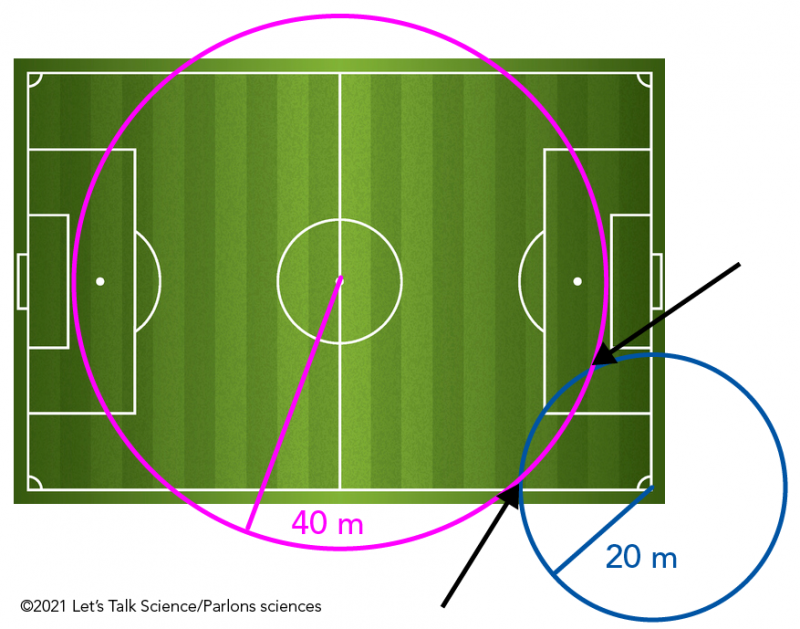
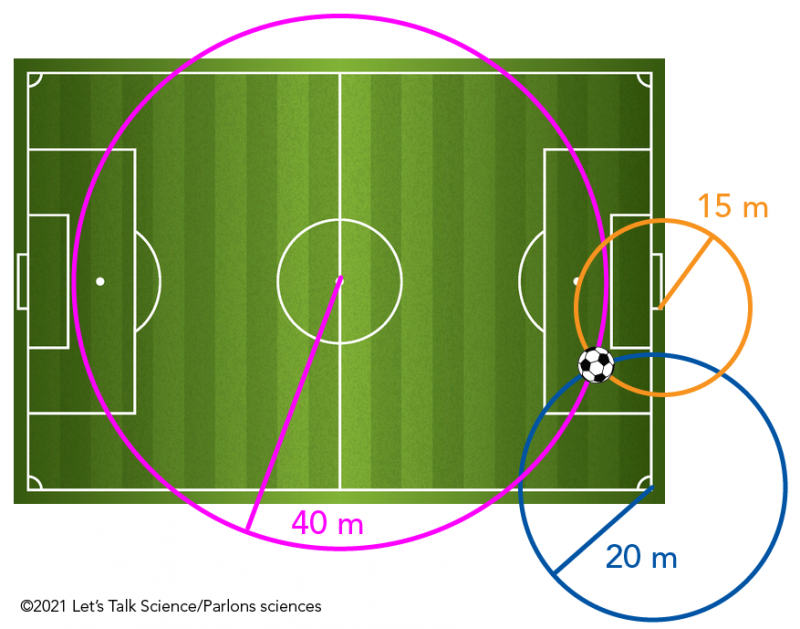
Here’s a simple example of how trilateration works. Imagine that you are standing on a soccer field. Next image that you are trying to find a ball on the field based on the following clues.
- The ball is 20m from the bottom right corner.
- The ball is 40m from the center of the field.
- The ball is 15m from the center of the left goal.
Based on these three clues, can you find the soccer ball?
Image - Text Version
Shown is an illustration of a soccer field. At the bottom right of the illustration is an outline of a blue circle that has its centre at the bottom right corner of the soccer field. The circle is identified as having a radius of 20 metres.
Image - Text Version
Shown is an illustration of a soccer field. At the bottom right is an outline of a blue circle that has its centre at the bottom right corner of the soccer field. The circle is identified as having a radius of 20 metres. In the centre of the illustration an outline of a pink circle that has its centre at the centre of the soccer field. The circle is identified as having a radius of 40 metres.
Image - Text Version
Shown is an illustration of a soccer field. At the bottom right is an outline of a blue circle that has its centre at the bottom right corner of the soccer field. The circle is identified as having a radius of 20 metres. In the centre of the illustration is an outline of a pink circle that has its centre at the centre of the soccer field. The circle is identified as having a radius of 40 metres. At the centre right of the illustration is an outline of an orange circle that has its centre at the centre of the goal net area. The circle is identified as having a radius of 15 metres. An image of a soccer ball overlaps the place on the soccer field where the lines of the three circles intersect.
Image - Text Version
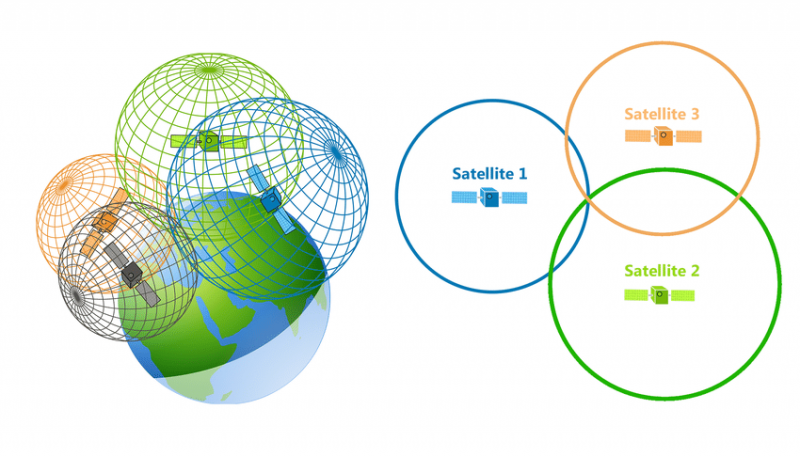
Show is an illustration of 2D and 3D trilateration.
On the left is an image of the Earth with four satellites flying above it. The satellites are coloured green, purple, orange and blue. Each satellite is surrounded by a sphere in the same colour as the satellite. The four spheres overlap slightly.
On the left is an image of three satellites. The satellites are coloured blue, orange and green. Each is centred in a circle that is drawn in the same colour as the satellite. There is one point where the three circles intersect.
Watch the video below to learn more.
(Please Note: The following video appears with a thumbnail that typically indicates a 'broken video' on YouTube, but the video works properly.)
As shown in the example above, trilateration only requires three satellites. So why do we need a fourth satellite? The fourth satellite adjusts for errors in the receiver’s clock. This makes GPS even more accurate. Currently, a GPS-enabled smartphone usually knows your location within about 5 metres.
Using satellite navigation has become a normal part of our daily life. Mapping apps help us find our way around the world. We use GPS for many social activities, such as geotagging posts or geocaching. First responders use GPS to quickly get to the location of an emergency and respond to disasters. GPS also helps planes safely get to their destination. Scientists use GPS to forecast the weather. These are just a few of the ways that we use this technology.
Next time you use GPS, take a minute to think about what makes this technology possible.
ANSWERS
- You cannot see the stars on a cloudy day or during the day.
- Winnipeg is located at 50 degrees North latitude. Hamilton is located at 80 degrees West longitude.
- 6 000 000 metres or 6 000 kilometres
Learn More
Trilateration Exercise
Practice your trilateration skills with activity from GPS.gov.
Navy Hidden Hero: Gladys Mae West and GPS
Watch this video to learn about one of the inventors of GPS.
How does your smartphone know your location?
Watch this video from TED-Ed to learn more about how satellites keep time so accurately.
References
AllAboutGPS (n.d.). The Global Positioning System (GPS). Retrieved from https://allaboutgps.weebly.com/math-behind-the-gps.html#
GISGeography (2021). How GPS Receivers Work: Trilateration vs. Triangulation. Retrieved from https://gisgeography.com/trilateration-triangulation-gps/
NASA Science: Space Place (2019). How does GPS work? Retrieved from https://spaceplace.nasa.gov/gps/en/
National Coordination Office for Space-Based Positioning, Navigation, and Timing (2021). GPS Accuracy. Retrieved from https://www.gps.gov/systems/gps/performance/accuracy/
NOAA (n.d.) The Global Positioning System: Global Positioning Tutorial. Retrieved from https://oceanservice.noaa.gov/education/tutorial_geodesy/geo09_gps.html
Singh, I. (2017, Jun. 17). Who invented the GPS? People behind the Global Positioning System. Geo Awesomeness. Retrieved from https://geoawesomeness.com/who-invented-the-gps/