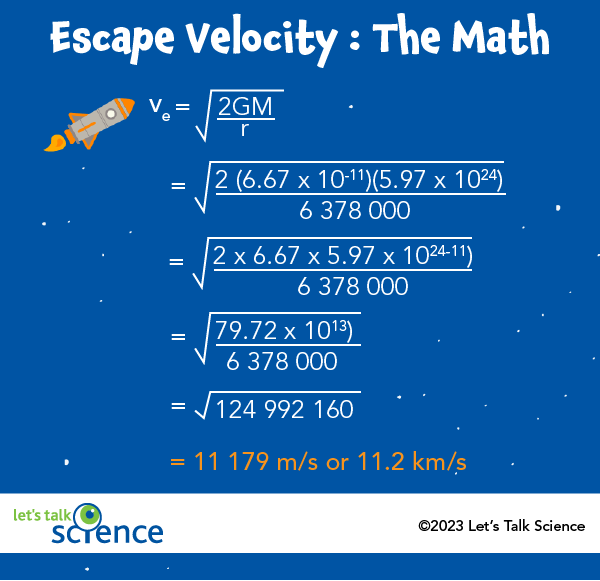
Escape Velocity

Artist’s conception of NASA’s Space Launch System (NASA).

Artist’s conception of NASA’s Space Launch System (NASA).
6.30
How does this align with my curriculum?
Curriculum Alignment
BC
11
Earth Sciences 11 (June 2018
Big Idea: Astronomy seeks to explain the origin and interactions of Earth and its solar system.
YT
11
Earth Sciences 11 (British Columbia, June 2018
Big Idea: Astronomy seeks to explain the origin and interactions of Earth and its solar system.
AB
10
Knowledge and Employability Science 10-4 (2006)
Unit B: Understanding Energy Transfer Technologies
BC
11
Physics 11 (June 2018)
Big Idea: An object’s motion can be predicted, analyzed, and described.
NU
10
Knowledge and Employability Science 10-4 (2006)
Unit B: Understanding Energy Transfer Technologies
YT
11
Physics 11 (British Columbia, June 2018)
Big Idea: An object’s motion can be predicted, analyzed, and described.
YT
12
Physics 12 (British Columbia, June 2018)
Big Idea: Measurement of motion depends on our frame of reference.