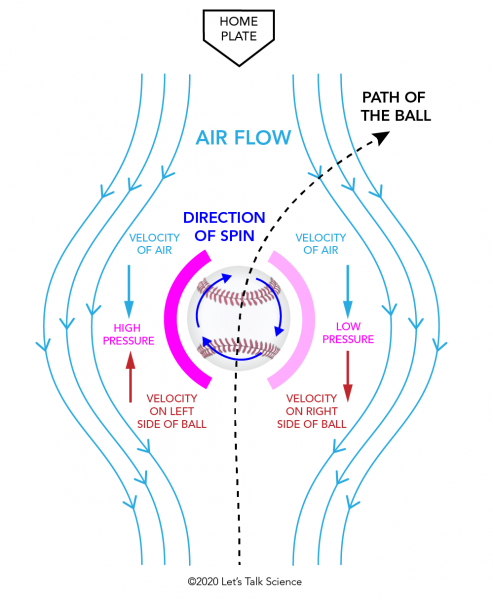
Why Do Curveballs Curve?

Pitcher holding a baseball (Pgiam, iStockphoto)

Pitcher holding a baseball (Pgiam, iStockphoto)
7.87
How does this align with my curriculum?
Curriculum Alignment
AB
10
Knowledge and Employability Science 10-4 (2006)
Unit B: Understanding Energy Transfer Technologies
BC
11
Physics 11 (June 2018)
Big Idea: An object’s motion can be predicted, analyzed, and described.
NU
10
Knowledge and Employability Science 10-4 (2006)
Unit B: Understanding Energy Transfer Technologies
YT
11
Physics 11 (British Columbia, June 2018)
Big Idea: An object’s motion can be predicted, analyzed, and described.
YT
12
Physics 12 (British Columbia, June 2018)
Big Idea: Measurement of motion depends on our frame of reference.
NT
10
Knowledge and Employability Science 10-4 (Alberta, 2006)
Unit B: Understanding Energy Transfer Technologies