What is a Fractal?

Saskatchewan River Delta, Manitoba (Elen11, iStockphoto)

Saskatchewan River Delta, Manitoba (Elen11, iStockphoto)
How does this align with my curriculum?
Learn about fractals and try making some yourself!

Image - Text Version
Shown is a colour computer drawing of the Barnsley Fern. The image is made up of branching green leaflets coming off a main green stalk. The leaflets get smaller and smaller as you move up the stem. The leaflets are exact copies of the fern as a whole, only on a smaller scale. They also get smaller as they move away from the stem.
When you look at the picture above, what do you see? Do you see the leaf of a fern plant, or do you see a complex, repeating pattern of ferns that seems to go on forever?
The image above is known as the Barnsely Fern. The Barnsley Fern is not a real fern, but rather an example of a fractal.
Did you know?
The Barnsley Fern is named after British mathematician Michael Barnsley who first described it in his book Fractals Everywhere.
Fractals are geometric figures, just like rectangles, circles and squares. But unlike those geometric figures, fractals have some special properties.
Properties of Fractals
Fractals are typically self-similar
Geometric objects, such as 2-dimensional figures, are similar if they have the same shape.
For example, the two squares on the left are similar because they have the same shape even though they are different sizes. The two rectangles on the right are NOT similar because they do not have the same shape.
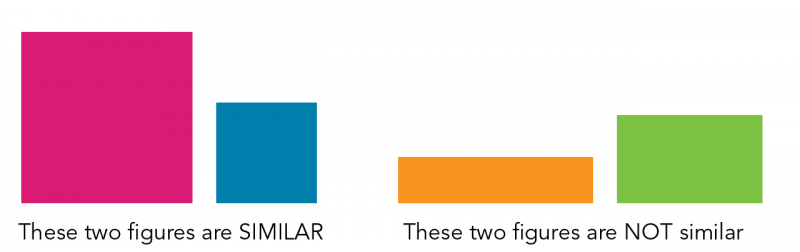
Image - Text Version
On the left side of the image are two squares. There is a larger magenta square and a smaller blue square. These two figures are considered to be similar to each other because they have the same shape. On the right side of the image are two rectangles. There is a short, wide orange rectangle and a taller, green rectangle. These two figures are not similar to each other because they do not have the same shape.
2-dimensional figures that are self-similar are made up of shapes that are smaller copies of the original shape. For example:
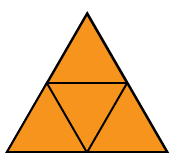
Image - Text Version
Illustration of an orange equilateral triangle. The triangle is divided into four smaller and similar equilateral triangles.

Image - Text Version
Illustration of a green square. The square is divided into four smaller and similar squares.
Question 1: Are hexagons self-similar? Can you form big hexagons out of smaller ones? Try it using pattern blocks. See the answer at the bottom of the page.
Fractals have repeating elements
One of the interesting things about fractals is that these self-similar shapes can be used to form patterns that can repeat over and over indefinitely! This is the other key part of what it means to be a fractal.

Image - Text Version
Three black and white checkboard patterns are shown. The far left is a 2 by 2 checkerboard, the centre image is a 4 by 4 checkerboard and the far right is an 8 x 8 checkerboard. In case you don't know, a checkerboard is an alternating black and white grid pattern.
Examples of Fractals
Sierpinski Triangle
One famous example of a fractal which is based on the self-similar shape of a triangle is the Sierpinski Triangle. This fractal is named after the Polish mathematician Wacław Sierpiński who described it in 1915. To create this fractal you:

Image - Text Version
A line drawing of a white equilateral triangle.
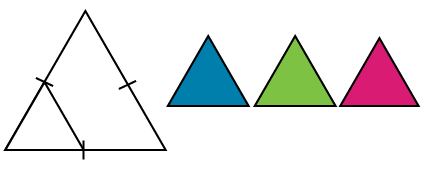
Image - Text Version
Four triangles are show. The triangle on the far left is a white line drawing. There are hash marks along each side showing where the mid point of each line. There is a line connecting two of the hash marks to showing a new half-sized triangle within the larger triangle. Beside the white triangle are three triangles that are half the size of the large, white triangle. One is shaded blue, one is shaded green and the third is shaded magenta.
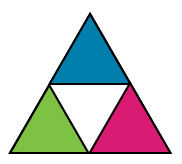
Image - Text Version
Shown is an outline of a large equilateral triangle. Within it are four smaller equilateral triangles that touch point to point. Three of the triangles fit in each corner of the large triangle and a fourth fits between them at the centre. The topmost small triangle is shaded blue, the centre triangel is white, the lower left triangle is shaded green and the lower right triangle is shaded magenta.
Did you know?
Another way to create this shape is to think about cutting a triangle-shaped hole out of the centre of each triangle.
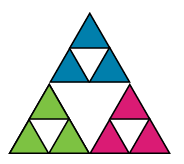
Image - Text Version
Shown is an image with three sets of triangles similar to the ones in step three. They are connected in such a way that they form a pyramid. The top most set of three triangles is shaded blue, the bottom left set of triangles is shaded green and the bottom right set of triangles is shaded magenta. As in step 3, there are white triangles centred within each group of coloured triangles.
Question 2: Draw and colour the next two Sierpinski triangles in this series. You will need a sharp pencil and a ruler. See the answer at the bottom of the page.
You can also make fractals based on shapes which are similar, but not self-similar. For example, a circle is not self-similar because it cannot be made up of smaller circles. However, you can make some interesting fractals using circles.
Apollonian Gasket
A famous fractal using circles is called the Apollonian Gasket. It is named after the Greek mathematician Apollonius of Perga (c. 262 BC – 190 BC).
To create this fractal you:
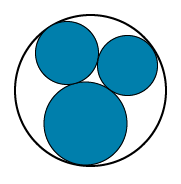
Image - Text Version
Shown is a black line drawing of a large circle. Within the circle are three other smaller circles that are just touching each other and the larger circle. The smaller circles are shaded blue.
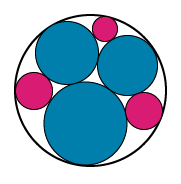
Image - Text Version
To the image above, three other circles are added. These even smaller circles are located in the white spaces between the initial three circles and the outer circle. The three additional circles are shaded magenta.
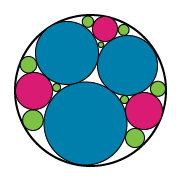
Image - Text Version
To the image above, nine other circles are added. These even smaller circles are located in the white spaces between the initial six circles and the outer circle. The nine additional circles are shaded green.
What makes this a fractal is that you can keep on adding smaller and smaller circles into the spaces an number of times.
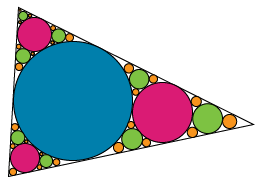
Image - Text Version
Shown is a black line drawing of a triangle filled in the same way as the examples above. The largest circle within it is shaded blue. The next smaller circles are shaded magenta, the next smaller circles are shaded green and the smallest circles are shaded orange.
Choose a shape and create your own Apollonian gasket-inspired work of art!
Koch Snowflake
It is also possible to make a fractal by changing the shape itself. A well known example of this is the Koch Snowflake. This fractal was first described by the Swedish mathematician Helge von Koch in 1904.
To create this shape:

Image - Text Version
Shown is a line drawing of an equilateral triangle. The line is coloured orange.
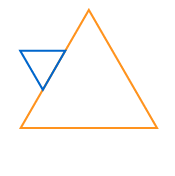

Image - Text Version
There are two images shown. In the top image is an orange line drawing of an equilateral triangle. Another equilateral triangle, one third the size of the orange triangle is connected edge to edge at the mid point on the left side of the orange triangle. The line of this smaller conencted triangle is blue.n the bottom image, the place where the two edges of the triangle connect has been removed. It now looks like there is a blue point coming out the side of the orange triangle.

Image - Text Version
Shown is a six-pointed star. The lines of three of the points are orange and the lines of the other three points are blue. Orange points alternate with blue points.
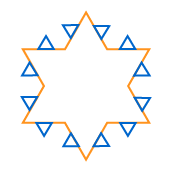

Image - Text Version
There are two images shown. The top image is a line drawing of an orange six pointed star. To each point has been added two smaller blue line drawings of triangles. Each of the smaller triangles is one third the size of the point of the star.
The bottom image is the same shape only this time the place where the edges where the triangles connect to the star has been removed. The shape now resembles an orange snowflake.

Image - Text Version
Shown is an orange line drawing of a shape that looks like an intricate snowflake. This shape has has 66 points.
By repeating this pattern many, many times, you have a fractal! Below is an animation of the first seven stages, or iterations, of the shape.
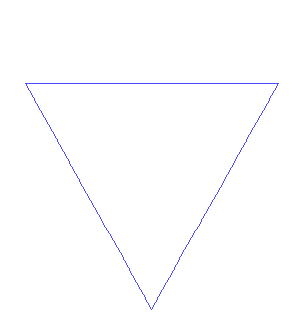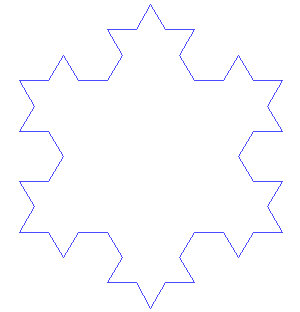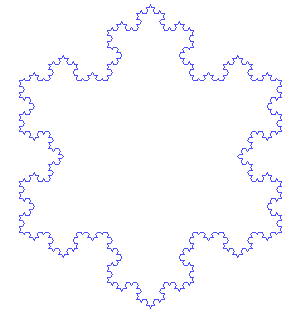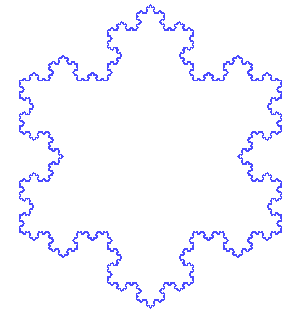
Animation of the first seven iterations of the Koch Snowflake (Source: Public domain image by António Miguel de Campos via Wikimedia Commons).
Image - Text Version
Animation of the first seven iterations of the Koch Snowflake.
Mandelbrot Set
The three fractals we have looked at so far are all created using a process known as iteration. Basically what this means is that you start with a specific shape and pattern, you adjust it and then you repeat it over and over again.
But this is not the only way to form fractals. One of the most famous fractals is the Mandelbrot Set. It is named after the mathematician Benoît Mandelbrot (1924 - 2010), who studied and made it popular. He discovered it when he noticed a self-similar repeating pattern in another set he was teaching called the Julia Set. He was only able to do this because he got access use some brand new IBM computers.

Just like with the Koch Snowflake, when you zoom in and look at the round shapes along the edges of the Mandelbrot set, they are self-similar!

When zooming in at the left hand shape of the Mandelbrot shape you can see the self-similarity (Source: Public domain image via Wikimedia Commons).
Misconception Alert
Images like the ones above were NOT drawn by hand! They were done on computers using complex mathematical equations to plot where points for the shapes can occur.
OPTIONAL: Learn More About the Math Behind the Mandelbrot Set
What is different about the Mandelbrot set fractal is that it is a set of numbers. For example, all of the natural numbers from one and five could be considered a set. We could show this using set notation. It would look like this:
{1, 2, 3, 4, 5}
Elements in sets are separated by commas and surrounded by curly brackets.
We can also describe this set in words, or semantic notation. In the case above, we could say, “Set A is a set of the first five natural numbers”.
Sets can contain both finite and infinite lists of numbers.
Set A = {1, 2, 3, 4, 5} (The first five natural numbers) is a finite set because there are only certain numbers that fit the rule “the first five natural numbers”.
We can also have infinite sets of numbers. For example, if our set was “all of the multiples of 3”, it could include an infinite list of numbers. We could show it in set notation and semantic notation as:
{3, 6, 9, 12, …} (the multiples of three)
There can be some very complex rules or functions applied to sets to generate the numbers within the set.
Say we wanted to create a set that was a sequence in which each number in the set was one natural number larger than the last. To do this we could use a recursive sequence. Essentially this means you take a number and apply a function to it to get the next number in the sequence. We use a bit of special notation to show this.
We use a variable called X and we use a little number below the X (a subscript) to indicate where the number is in the sequence.
The earlier example:
{1, 2, 3, 4, 5}
Could be re-written as:
{X1, X2, X3, X4, X5}
A number in the nth position in the sequence is Xn.
So, how could we use this notation to explain how to create the sequence from 1 to 5? This case is easy because the position in the sequence and the number are the same.
Xn = n
For the first number in the sequence X1 = 1. Does that match up? Yes! Try it yourself for X2, X3, X4 and X5.
Creating a pattern is pretty simple when the formula is easy like this one. But the formula can be much more complicated.
Question 3: Find the first five numbers in a sequence that has the pattern Xn = n2 + 1. See the answer at the bottom of the page.
The Mandelbrot set uses some pretty complicated rules for both the function and where the numbers can and cannot start. It even uses real as well as imaginary numbers!
If you are interested in learning more, check out the links in the Learn More section below.
Fractals in Everyday Life
Fractals in Nature

Fractal in Art
The second answer has to do with the ‘beauty’ of fractals. People seem to be fascinated by fractals! Try doing a web search for fractal art and exploring some of the amazing galleries of images people have created with different fractals.
Or, try a web search for fractal music and you will find music people have created using fractals. Instead of creating images, they create self-similar, repeating patterns with musical notes. Just like when looking at fractal images, when listening to fractal music, it’s often easy to forget it was made from a set of mathematical equations!
Someone else even turned areas in the Mandelbrot set, as well as other cool fractals, into sounds!
Practical Applications of Fractals
Fractals have also been used for many practical purposes. Geologists use fractal geometry to understand how oil flows through underground reservoirs as well as to locate oil deposits. They also use fractals to create models of how earthquakes work.
Engineers have used fractal geometry for stress testing on oil rigs and aircraft. In medicine, fractal geometry has been used to study the walking patterns of patients with Parkinson’s disease in order to understand the severity of their symptoms.
The military uses fractals to identify human-made versus nature features on aerial maps and fractals have been used to design better camouflage for military uniforms. Scientists have also used fractals to search for artificial objects on planetary surfaces.
Fractals and Climate Change
Fractals are also being used to help us better understand the Earth and the impacts of climate change. Understanding the shapes and sizes of things such as clouds, forests, ponds, and shorelines can help scientists more accurately model climate systems and the impact that climate change has on these systems.
For example, fractals can help researchers understand the surface areas of very irregular shapes, such as the shape of a leaf or the cover of a forest. This can help them make better estimates of things like carbon capture through photosynthesis. To do this they use something called fractal dimensions. Essentially what this means is that the smaller the scale you use to measure something, the more accurate the measurement is.
For example, say we wanted to measure the area and perimeter of an island that had an irregular shape. How would we do this? One way would be to make squares of a certain size and see how many would cover the shape of the island. It is important to note that we are only counting squares that only cover the land and not the water.
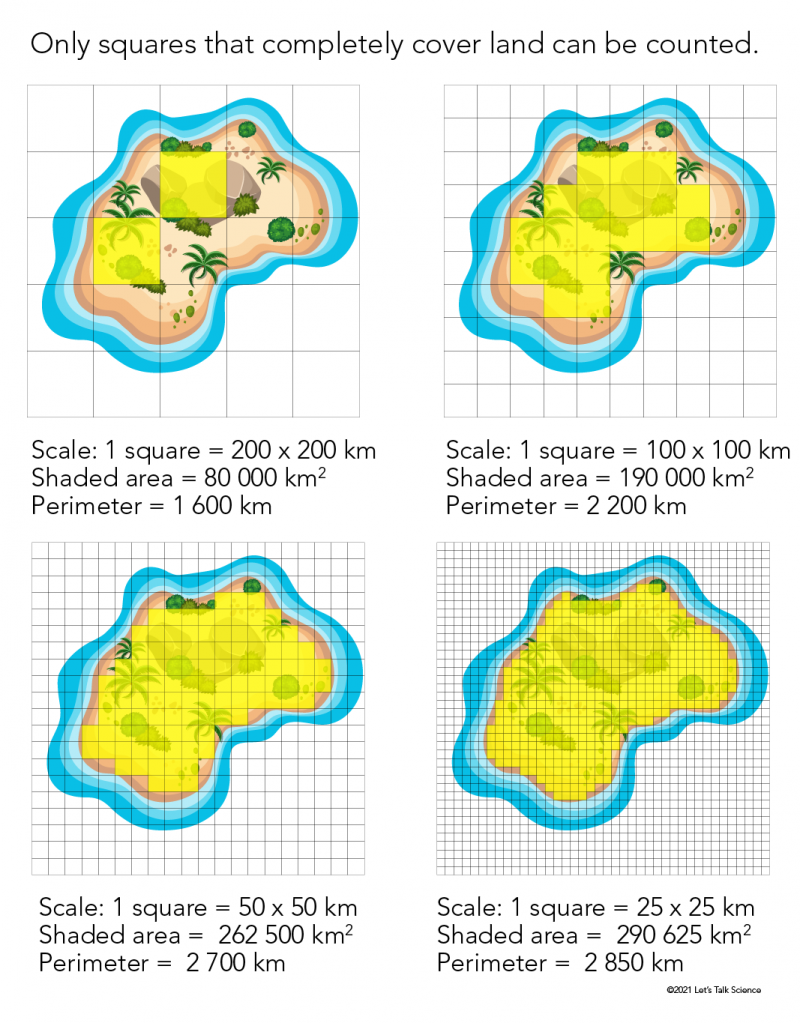
Image - Text Version
Shown are four images of the same illustration of an irregularly shaped tropical island. Overlayed on each is a grid.
On the top left island, a five by five grid overlays the island. Any part of the island that is completely within one of the grid squares is shaded yellow. For this island, two squares are shaded. The scale of the grid is 200 by 200 kilometres. As a result, this island has a shaded area of 190 000 square kilometers and a perimeter of 1 600 km.
On the top right island, a 10 by 10 grid overlays the island. Any part of the island that is completely within one of the grid squares is shaded yellow. For this island, 19 squares are shaded. The scale of the grid is 100 by 100 kilometres. As a result, this island has a shaded area of 80 000 square kilometers and a perimeter of 2 200 km.
On the bottom left island, a 20 by 20 grid overlays the island. Any part of the island that is completely within one of the grid squares is shaded yellow. For this island, 105 squares are shaded. The scale of the grid is 50 by 50 kilometres. As a result, this island has a shaded area of 262 500 square kilometers and a perimeter of 2 700 km.
On the bottom right island, a 40 by 40 grid overlays the island. Any part of the island that is completely within one of the grid squares is shaded yellow. For this island, 465 squares are shaded. The scale of the grid is 25 by 25 kilometres. As a result, this island has a shaded area of 290 625 square kilometers and a perimeter of 2 950 km.
When the squares are big, we cannot put on very many squares. But if we were to use smaller squares, we could put on more. We could keep going, using smaller and smaller squares. The smaller the squares, the closer we are to the actual size of the island. What do you think would be the smallest size square you could use? Technically there isn’t one. You could keep on making smaller and smaller squares forever! This is what makes this type of measurement a fractal. As you can see in the image below, as we make the size of the squares we are using to measure smaller, we cover more of the area of the island. This should remind you of the Koch snowflake!
Fractals are everywhere, when you know where to look!
ANSWERS
Q1: No, hexagons are not self-similar in the same way as squares and equilateral triangles.

Image - Text Version
Shown are five images of hexagons in a line. The first hexagon has a black outline and is shaded in light blue. The second hexagram is filled with seven smaller hexagon shaded purple. Six small hexagons fit into the hexagons vertices and the seventh is in the centre. Parts of the large hexagon not covered by the small hexaon are shaded light blue. The third hexagon also has seven smaller hexagons within it. They are shaded red. This time the six hexagons each have an edge touching the outer edge of the large hexagon. The seventh hexagon fits completely within the othe six small hexagons. Parts of the large hexagon not covered by the small hexaon are shaded light blue. The fourth large hexagon has three hexagons within it. They are shaded dark blue. They fit into three alternating vertices of the large hexagon. Parts of the large hexagon not covered by the small hexaon are shaded light blue. The fifth hexagon is divided by black lines that run horizontally and diagonally forming rows of hexagons. This hexagon is also shaded light blue.
Q2: The next two Sierpiński Triangles in this series would look like this.
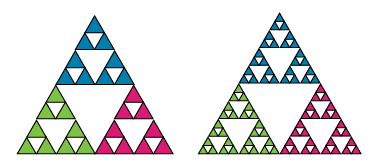
Image - Text Version
Two images are shown. The image on the left is a Sierpinki triangle created from 27 smaller triangles and the the image on the right is a Sierpinki triangle created from 81 smaller triangles. In each of the three vertex groups, the triangles are coloured the same. The upper area has triangles shaded blue, the lower left area has triangles shaded green and the lower right area has triangles shaded magenta.
Q3: First five numbers that fit the pattern Xn = n2 + 1
X1 = (1)2 + 1 = 2
X2 = (2)2 + 1 = 5
X3 = (3)2 + 1 = 10
X4 = (4)2 + 1 = 17
X5 = (5)2 + 1 = 26
{2, 5, 10, 17, 26}
Learn More
The Fractal Foundation
The Fractal Foundation website has pictures, videos, activities, and free software for creating your own fractals.
Koch Snowflake - Khan Academy
This video from Khan Academy explains how to create a Koch Snowflake as well as the math behind its perimeter and area.
The Sierpinski Triangle
This section of the Fractals module from Mathigon let’s you learn about and play with interactive Sierpinski Triangles.
Fractal Trianglethon
Why not make your own giant Sierpinski Triangle like the kids did at the Fractal Trianglethon (Fractal Foundation). Their website has some other interesting information about fractals.
The Mandelbrot Set
This section of the Fractals module from Mathigon let’s you learn about and play with both the Julia Set and the Mandelbrot set.
Fractal Zoom Mandelbrot Corner
This YouTube video (1:40 min.) has an animation which zooms in on the Mandelbrot set.
14 Amazing Fractals Found in Nature
This web page, from Treehugger.com, has images of some amazing fractals and how they are created.
Make Fractal Art With Python! (2021)
In this YouTube video (34:29 min.) learn how to create fractal art using Python and the turtle module.
References
Acuna, J. A. and Y. C. Yortsos (1995). Application of Fractal Geometry to the Study of Networks of Fractures and their Pressure Transient. Water Resources Research 31 (3): 527-540
Bhattacharya, P, B.K. Chakrabart, Kamal, and D. Samanta (2009). Fractal Models of Earthquake Dynamics. arXiv.org. Retrieved from https://arxiv.org/ftp/arxiv/papers/0906/0906.1931.pdf
Cai, J, L. Zhang, Y. Ju, G. Pia and Z. Zhang (2018). An introduction to fractal-based approaches in unconventional reservoirs - Part 1. Fractals 26 (2): 1-4
Carlotto, M. J. and M. C. Stein (1990). A method for searching for artificial objects on planetary surfaces. Journal of the British Interplanetary Society 43: 209-216
Gascueña, D. (2020). Applied Fractal Geometry: from Climate Change to Cancer. Open Mind BBVA. Retreived from https://www.bbvaopenmind.com/en/science/mathematics/applied-fractal-geometry-from-climate-change-to-cancer/
Institute of Physics (2004). Physicists Use Fractals To Help Parkinson’s Sufferers. Science Daily. Retrieved from https://www.sciencedaily.com/releases/2004/02/040203232954.htm
Marion, B. (n.d.) Fractals For Dummies. Retrieved from https://brunomarion.com/fractals-for-dummies/
MITK12Videos. (11 June 2015). What Is A Fractal (and what are they good for)? [Video]. Youtube. https://www.youtube.com/watch?v=WFtTdf3I6Ug
Norimer, N.D., R.G. Haight and R.A. Leary (1994). The Fractal Forest: Fractal Geometry and Applications in Forest Science. St. Paul, MN: U.S. Department of Agriculture, Forest Service, North Central Forest Experimental Station.